 |
A C. 1727. feladat (2022. május) |
C. 1727. Fúrjunk át egy \(\displaystyle R\) sugarú tömör gömböt egy, a gömb középpontján átmenő egyenes mentén egy \(\displaystyle r\) sugarú hengeres fúróval, ahol \(\displaystyle r<R\). Fejezzük ki a keletkezett maradéktest térfogatát a maradéktest \(\displaystyle m\) magasságának függvényében.
Javasolta: Szabó Bertalan (Miskolc, 1986)
(5 pont)
A beküldési határidő 2022. június 10-én LEJÁRT.
Megoldás. Messük el a gömböt a gömb \(\displaystyle O\) középpontján átmenő olyan síkkal, amely a henger \(\displaystyle t\)-vel jelölt tengelyét tartalmazza. Ez a sík a gömbből kimetszi a \(\displaystyle 2R\) átmérőjű kört, a hengerből pedig az \(\displaystyle ABCD\) téglalapot. Az \(\displaystyle ABCD\) téglalap oldalaira \(\displaystyle AB=CD=2r\) és \(\displaystyle BC=DA=m\) teljesül. Tekintsük az alábbi ábrát.
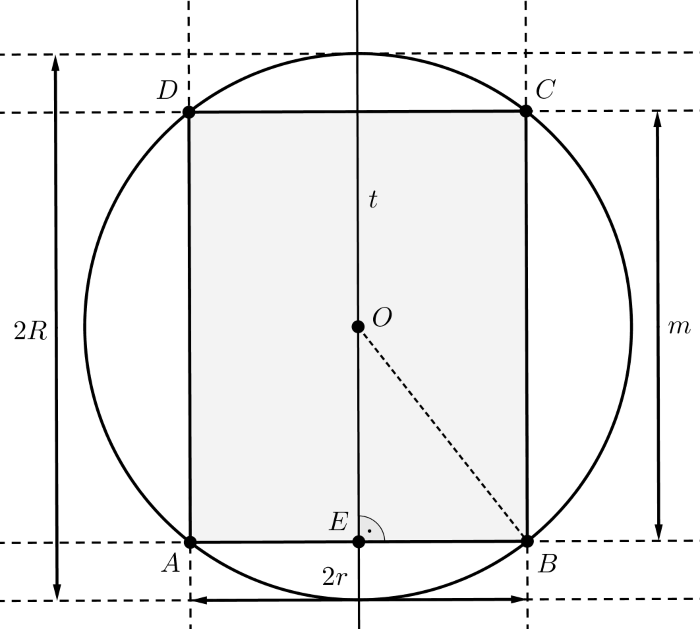
A gömbnek a feladatban leírt átfúrása után a gömbből hiányozni fog egyrészt az a két gömbsüveg, amelyek alaplapja az \(\displaystyle AB\), illetve \(\displaystyle CD\) átmérőjű kör, magassága pedig \(\displaystyle \displaystyle{h=R-\frac{m}{2}}\), másrészt pedig a henger, amelynek alapköre \(\displaystyle r\) sugarú, magassága \(\displaystyle m\). A gömb térfogata \(\displaystyle \displaystyle{V_g=\frac{4R^3\cdot{\pi}}{3}}\), a henger térfogata \(\displaystyle \displaystyle{V_h=r^2\cdot{\pi}\cdot{m}}\), az \(\displaystyle R\) sugarú gömbből levágott és \(\displaystyle r\) sugarú alapkörrel rendelkező, \(\displaystyle h\) magasságú gömbsüveg térfogata \(\displaystyle \displaystyle{V_s=\frac{\pi\cdot{h^2}\cdot{\big(3R-h\big)}}{3}}\).
A gömb átfúrása után keletkező maradéktest térfogata
\(\displaystyle \displaystyle{V_m=V_g-2V_s-V_h},\)
azaz
| \(\displaystyle (1)\) | \(\displaystyle \displaystyle{V_m=\frac{4R^3\cdot{\pi}}{3}-\frac{2\pi\cdot{h^2}\cdot{\big(3R-h\big)}}{3}}-r^2\cdot{\pi}\cdot{m}.\) |
Az (1) egyenlet jobb oldalán kiemeljük a \(\displaystyle \displaystyle{\frac{\pi}{3}}\) tényezőt és beírjuk a \(\displaystyle \displaystyle{h=R-\frac{m}{2}}\) összefüggést:
\(\displaystyle \displaystyle{V_m=\frac{\pi}{3}\cdot{\Bigg[4R^3-2\Big(R-\frac{m}{2}\Big)^2\cdot{\Big(2R+\frac{m}{2}\Big)}-3r^2\cdot{m}\Bigg]}}.\)
A műveletek elvégzése és rendezés után azt kapjuk, hogy
| \(\displaystyle (2)\) | \(\displaystyle \displaystyle{V_m=\frac{\pi}{3}\cdot{\Bigg[3R^2m-\frac{m^3}{4}-3r^2m}\Bigg]}.\) |
Írjuk fel most az ábra \(\displaystyle OEB\) derékszögű háromszögére a Pitagorasz-tételt, eszerint \(\displaystyle \displaystyle{r^2+\frac{m^2}{4}=R^2}\), ezt a (2) egyenletbe helyettesítve a műveletek elvégzése és egyszerűsítés után adódik, hogy
\(\displaystyle \displaystyle{V_m=\frac{\pi\cdot{m^3}}{6}},\)
ezzel megadtuk a maradéktest térfogatát az \(\displaystyle m\) magasságának függvényében.
Statisztika:
22 dolgozat érkezett. 5 pontot kapott: Cynolter Dorottya, Horváth Milán, Keszthelyi Eszter, Kurucz Márton, Nagy Daniella, Pekk Márton, Szabó Réka, Szalanics Tamás, Waldhauser Miklós, Werner Kinga. 2 pontot kapott: 1 versenyző. 1 pontot kapott: 7 versenyző. 0 pontot kapott: 3 versenyző.
A KöMaL 2022. májusi matematika feladatai

