Problem C. 1736. (October 2022)

C. 1736. Let \(\displaystyle P\) be an interior point of side \(\displaystyle CD\) of a parallelogram \(\displaystyle ABCD\), and let \(\displaystyle Q\) be an interior point of side \(\displaystyle AB\) (being parallel with \(\displaystyle CD\)). The line segments \(\displaystyle PA\) and \(\displaystyle QD\) intersect each other at \(\displaystyle M\), while the line segments \(\displaystyle PB\) and \(\displaystyle QC\) intersect each other at \(\displaystyle N\). Find a condition to have \(\displaystyle MN\parallel{AB}\).

(Based on a U.S. mathematics competition problem)

(5 pont)

Deadline expired on November 10, 2022.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Legyen az \(\displaystyle ABCD\) paralelogramma \(\displaystyle AB\) és \(\displaystyle CD\) oldalának hossza \(\displaystyle a\), valamint legyen \(\displaystyle PD=x\), illetve \(\displaystyle QA=y\), ezzel \(\displaystyle PC=a-x\), illetve \(\displaystyle QB=a-y\).

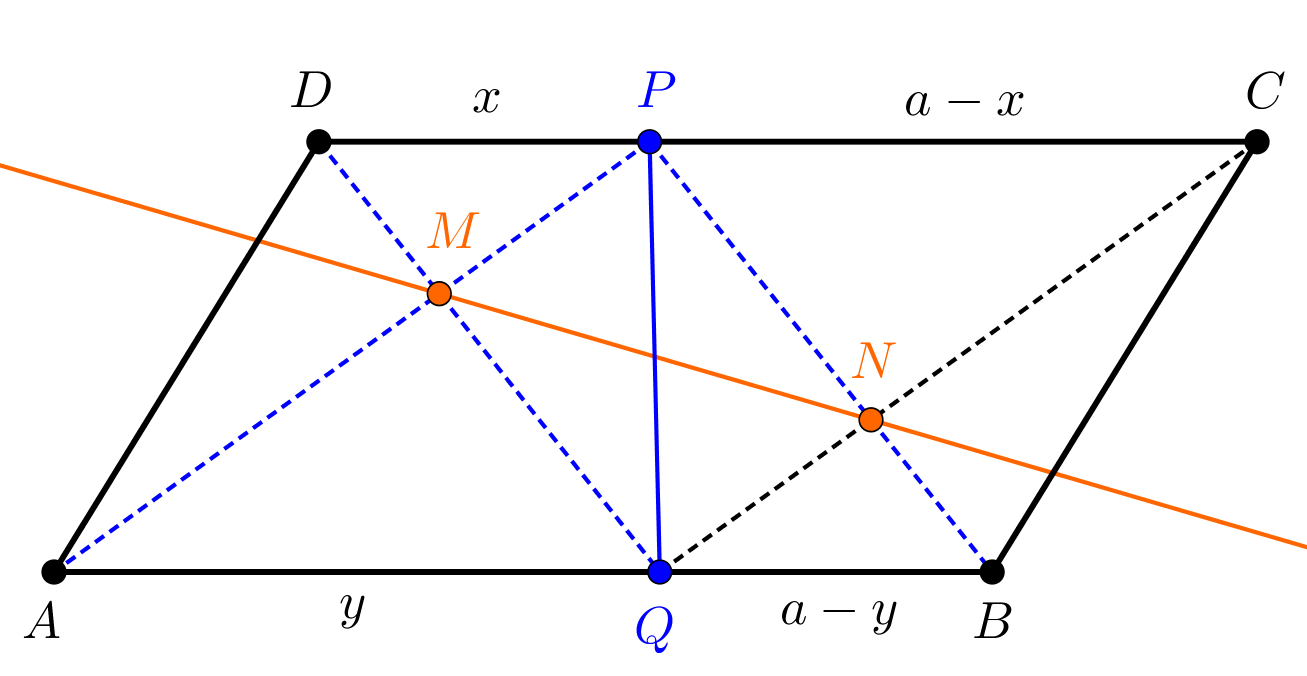
A feltételekből következik, hogy az \(\displaystyle ABP\) háromszög és az \(\displaystyle AP\), illetve \(\displaystyle BP\) oldalakat metsző \(\displaystyle MN\) egyenes mindig létrejön.

Az \(\displaystyle MN\) egyenes akkor és csak akkor párhuzamos \(\displaystyle AB\)-vel, ha teljesül, hogy

Ha ugyanis fennáll (1), akkor a párhuzamos szelők tételének megfordításából következik, hogy \(\displaystyle MN\parallel{AB}\), ha pedig \(\displaystyle MN\parallel{AB}\), akkor a párhuzamos szelők tétele miatt teljesül az (1) egyenlőség.

Elegendő az (1) összefüggés helyett tanulmányozni a

egyenlőséget, mert \(\displaystyle PA=PM+MA\), illetve \(\displaystyle PB=PN+NB\) felhasználásával egyszerűen belátható, hogy (1) és (2) ekvivalensek.

Nyilvánvaló, hogy \(\displaystyle AQPD\) és \(\displaystyle CPQB\) trapézok, átlóik metszéspontjai éppen \(\displaystyle M\) és \(\displaystyle N\).

Ismeretes, hogy a trapézok átlóinak metszéspontja az átlókat a párhuzamos oldalak arányában osztja, ezért az \(\displaystyle AQPD\) trapézban \(\displaystyle \displaystyle{\frac{PM}{MA}=\frac{x}{y}}\), a \(\displaystyle CPQB\) trapézban pedig \(\displaystyle \displaystyle{\frac{PN}{NB}=\frac{a-x}{a-y}}\).

Eszerint (2) pontosan akkor teljesül, ha

\(\displaystyle \displaystyle{\frac{x}{y}=\frac{a-x}{a-y}},\)

amelyből egyszerű átalakításokkal azt kapjuk, hogy \(\displaystyle x=y\).

Eszerint \(\displaystyle MN\parallel{AB}\) akkor és csak akkor áll fenn, ha a \(\displaystyle PD\) és \(\displaystyle AQ\) szakaszok hossza egyenlő, ekkor természetesen \(\displaystyle PC=BQ\) is igaz.

Eredményünk azt is jelenti, hogy ebben az esetben az \(\displaystyle AQPD\) és \(\displaystyle CPQB\) négyszögek paralelogrammák.

Megjegyzés. Az, hogy a trapéz átlóinak metszéspontja az átlókat a párhuzamos oldalak arányában osztja, a Geometriai feladatgyűjtemény I. kötetének 1233. számú feladata.

Statistics:

51 students sent a solution.
5 points:	Baksa Anna, Berta Botond, Bezsilla Gábor, Dancsák Dénes, Göncző Emma, Hajós Balázs, Halász Henrik, Heltovics Lilla, Hüvös Gergely, Kéki Edit, Keszthelyi Eszter, Mészáros Anna Veronika, Pekk Márton, Prikler Dorka Abigél, Richlik Márton, Ruzsa Bence Márk, Seprődi Barnabás Bendegúz, Szittyai Anna, Varga Dániel 829, Végh Lilian.
4 points:	Hosszu Noel, Sipeki Márton, Waldhauser Miklós.
3 points:	6 students.
2 points:	2 students.
1 point:	1 student.
0 point:	3 students.
Unfair, not evaluated:	7 solutionss.

Problems in Mathematics of KöMaL, October 2022