 Problem C. 1740. (November 2022)
Problem C. 1740. (November 2022)
C. 1740. \(\displaystyle P\) is an interior point of side \(\displaystyle CD\) of a parallelogram \(\displaystyle ABCD\), and \(\displaystyle Q\) is an interior point of side \(\displaystyle AB\) parallel to \(\displaystyle CD\). The intersection of line segments \(\displaystyle PA\) and \(\displaystyle QD\) is \(\displaystyle M\), and the intersection of line segments \(\displaystyle PB\) and \(\displaystyle QC\) is \(\displaystyle N\).
Assume that \(\displaystyle MN\nparallel{AB}\), and \(\displaystyle MN\) intersects the line of \(\displaystyle CD\) at point \(\displaystyle X\), and the line of \(\displaystyle AB\) at point \(\displaystyle Y\). Prove that \(\displaystyle DX=BY\).
(American competition problem)
(5 pont)
Deadline expired on December 12, 2022.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Legyen az \(\displaystyle ABCD\) paralelogramma \(\displaystyle AB\) és \(\displaystyle CD\) oldalának hossza \(\displaystyle a\), valamint legyen \(\displaystyle DX=x\), illetve \(\displaystyle BY=y\). Azt kell bizonyítanunk, hogy \(\displaystyle x=y\). Ehhez tekintsük a következő ábrát.
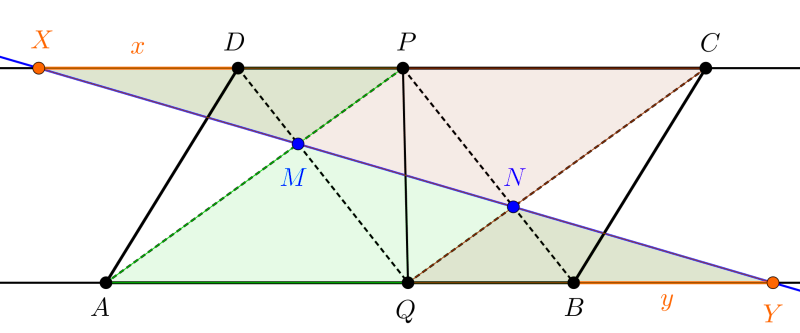
A feltételekből következik, hogy az \(\displaystyle M\) és az \(\displaystyle N\) metszéspontok mindig létrejönnek, és minden lehetséges esetben különböznek is egymástól, így a \(\displaystyle P, Q\) pontok bármely, a feltételnek megfelelő elhelyezése esetén az \(\displaystyle MN\) egyenes is mindig létezik és mivel \(\displaystyle MN\nparallel{AB}\), ezért az \(\displaystyle X, Y\) metszéspontok is létrejönnek.
Az \(\displaystyle AQPD\) és \(\displaystyle CPQB\) négyszögek trapézok, átlóik metszéspontja \(\displaystyle M\), illetve \(\displaystyle N\).
A trapéz átlóinak metszéspontja az átlókat a párhuzamos oldalak arányában osztja, ezért az \(\displaystyle AQPD\) trapézban
| \(\displaystyle (1)\) | \(\displaystyle \displaystyle{\frac{PM}{MA}=\frac{PD}{AQ}},\) |
a \(\displaystyle CPQB\) trapézban pedig
| \(\displaystyle (2)\) | \(\displaystyle \displaystyle{\frac{CN}{NQ}=\frac{CP}{BQ}=\frac{a-PD}{BQ}}.\) |
Az \(\displaystyle AB\) és \(\displaystyle CD\) egyenesek párhuzamossága miatt az \(\displaystyle XMP\) és \(\displaystyle YMA\) háromszögek megfelelő szögei egyenlők, ezért a két háromszög hasonló, és így az (1) egyenlet felhasználásával
| \(\displaystyle (3)\) | \(\displaystyle \displaystyle{\frac{PM}{MA}=\frac{PD}{AQ}=\frac{x+PD}{a+y}}.\) |
Hasonló módon láthatjuk be, hogy az \(\displaystyle XNC\) és \(\displaystyle YNQ\) háromszögek is hasonlók, ezért (2) szerint
| \(\displaystyle (4)\) | \(\displaystyle \displaystyle{\frac{CN}{NQ}=\frac{CP}{BQ}=\frac{a-PD}{BQ}=\frac{a+x}{y+BQ}}.\) |
A műveletek elvégzésével és rendezéssel a (3) egyenletből azt kapjuk, hogy
| \(\displaystyle (5)\) | \(\displaystyle \displaystyle{x\cdot{AQ}+PD\cdot{AQ}=PD\cdot{a}+PD\cdot{y}},\) |
a (4) egyenletből pedig azt, hogy
| \(\displaystyle (6)\) | \(\displaystyle \displaystyle{x\cdot{BQ}+PD\cdot{BQ}=y\cdot{a}-PD\cdot{y}}.\) |
Az (5) és (6) egyenletek megfelelő oldalait összeadva és figyelembe véve, hogy \(\displaystyle AQ+BQ=a\), adódik az
\(\displaystyle \displaystyle{x\cdot{a}+PD\cdot{a}=y\cdot{a}+PD\cdot{a}}\)
egyenlőség, ahonnan rendezés, és a pozitív \(\displaystyle a\) számmal való osztás után
\(\displaystyle x=y\)
következik, amit bizonyítani akartunk.
Megjegyzés. Ha az \(\displaystyle ABCD\) átlóinak metszéspontját \(\displaystyle K\)-val jelöljük, akkor könnyen bizonyítható, hogy az \(\displaystyle XDK\) és \(\displaystyle YBK\) háromszögek egybevágók, ezért az \(\displaystyle X, K, Y\) pontok egy egyenesre illeszkednek. Ez azt is jelenti, hogy az \(\displaystyle MN\) egyenes áthalad a paralelogramma \(\displaystyle K\) szimmetriaközéppontján.
Statistics:
82 students sent a solution. 5 points: Balogh Péter, Bérczes Botond, Hajós Balázs, Halász Henrik, Iván Máté Domonkos, Kerekes András, Keszthelyi Eszter, Kővágó Edit Gréta, Ligeti Ábel, Németh Hanna Júlia , Sütő Áron, Szabó Donát, Ujpál Bálint. 4 points: Kriston Nándor, Prikler Dorka Abigél, Schneider Dávid. 3 points: 5 students. 2 points: 11 students. 1 point: 31 students. 0 point: 4 students. Unfair, not evaluated: 7 solutionss. Not shown because of missing birth date or parental permission: 1 solutions.
Problems in Mathematics of KöMaL, November 2022
