 Problem C. 1754. (February 2023)
Problem C. 1754. (February 2023)
C. 1754. Squares \(\displaystyle ABCD, BEFC\) and \(\displaystyle EGHF\) are drawn next to each other in a plane. The foot of the perpendicular drawn from \(\displaystyle B\) to \(\displaystyle DE\) is \(\displaystyle K\). Show that the points \(\displaystyle A\), \(\displaystyle K\), \(\displaystyle H\) are collinear.
Proposed by B. Bíró, Eger
(5 pont)
Deadline expired on March 10, 2023.
Sorry, the solution is available only in Hungarian. Google translation
1. megoldás. Helyezzük el a három egymás melletti négyzetet úgy, hogy az \(\displaystyle A\) pont az origóba, a \(\displaystyle B\) pont az \(\displaystyle x\)-tengelyre kerüljön és legyen a négyzetek oldalának hossza \(\displaystyle a\). Ekkor a négyzetek csúcsainak koordinátái:
| \(\displaystyle (1)\) | \(\displaystyle A(0;0),\quad B(a;0),\quad C(a;a),\quad D(0;a),\quad E(2a;0),\quad F(2a;a),\quad G(3a;0),\quad H(3a;a).\) |
Tekintsük az 1. ábrát, amelyen az \(\displaystyle AH\) és \(\displaystyle DE\) szakaszok metszéspontját \(\displaystyle K'\)-vel jelöltük.
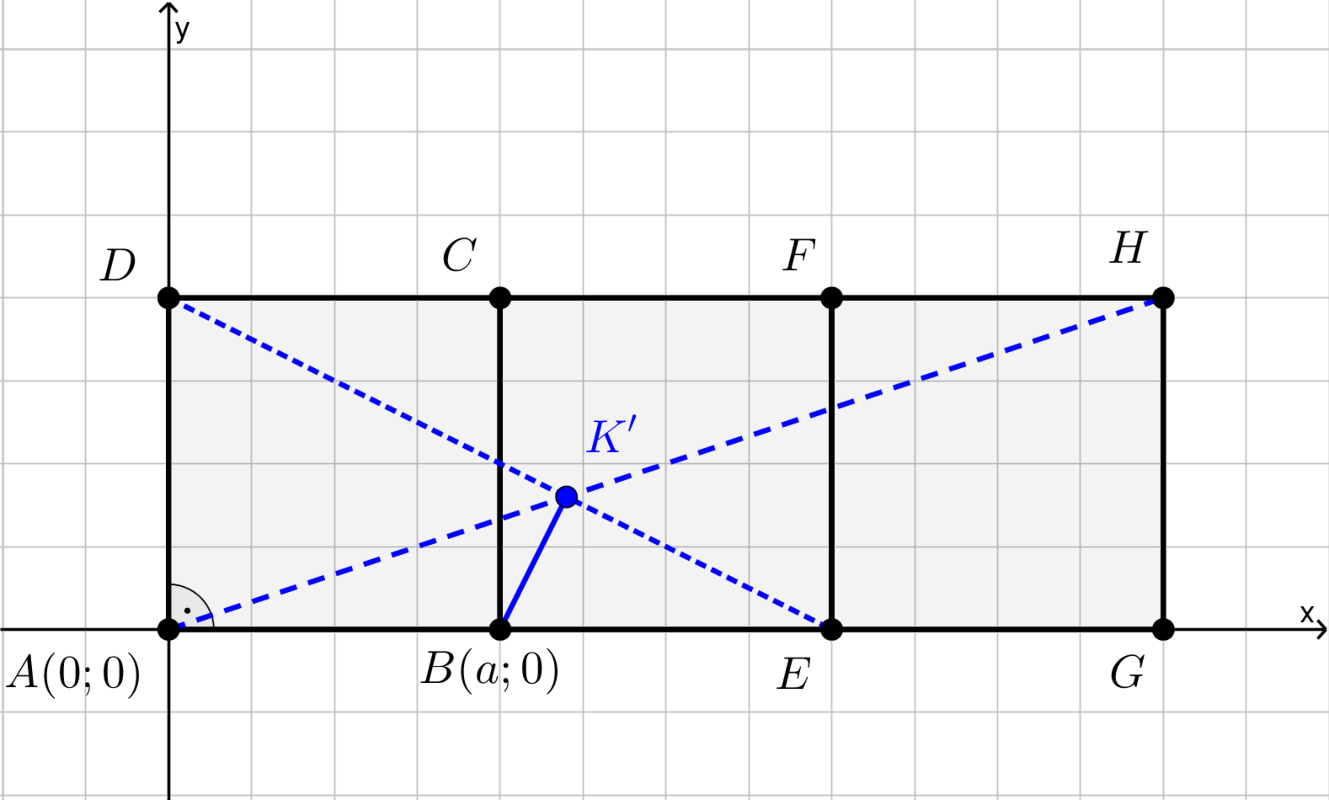
1. ábra
Elegendő bizonyítani, hogy \(\displaystyle BK'\) merőleges \(\displaystyle DE\)-re, mert ekkor nyilvánvaló, hogy \(\displaystyle K=K'\) és így az \(\displaystyle A, K, H\) pontok valóban egy egyenesre esnek.
Az origón áthaladó \(\displaystyle AH\) egyenes meredeksége (1) felhasználásával \(\displaystyle \displaystyle{\frac{a}{3a}=\frac{1}{3}}\), ezért egyenlete
| \(\displaystyle (2)\) | \(\displaystyle y=\frac{1}{3}x.\) |
Hasonlóképpen a \(\displaystyle DE\) egyenes meredeksége (1) szerint \(\displaystyle \displaystyle{-\frac{a}{2a}=-\frac{1}{2}}\), tehát az egyenes egyenlete
| \(\displaystyle (3)\) | \(\displaystyle y=-\frac{1}{2}x+a.\) |
A (2) és (3) egyenletekből álló egyenletrendszer megoldása az
| \(\displaystyle (4)\) | \(\displaystyle \displaystyle{x=\frac{6a}{5};\quad y=\frac{2a}{5}}\) |
számpár, ezek a \(\displaystyle K'\) pont koordinátái.
A \(\displaystyle BK'\) egyenes egy irányvektora \(\displaystyle \displaystyle{\overrightarrow{BK'}\bigg(\frac{a}{5}; \frac{2a}{5}\bigg)}\), ezért a \(\displaystyle BK'\) egyenes meredeksége
| \(\displaystyle (5)\) | \(\displaystyle m_{BK'}=2.\) |
Két olyan egyenes, amelynek van meredeksége, pontosan akkor merőleges egymásra, ha a meredekségeik szorzata \(\displaystyle -1\). A \(\displaystyle DE\) és \(\displaystyle BK'\) egyenesek meredekségének szorzata (3), illetve (5) alapján éppen \(\displaystyle -1\), tehát a \(\displaystyle DE\) és \(\displaystyle BK'\) egyenesek merőlegesek egymásra.
Ezt azt jelenti, hogy \(\displaystyle K=K'\) valóban teljesül, ezért az \(\displaystyle A, K, H\) pontok egy egyenesen vannak.
2. megoldás. A feladatot úgy oldjuk meg, hogy kiszámítjuk a \(\displaystyle KA\) és \(\displaystyle KH\) távolságokat, és igazoljuk, hogy \(\displaystyle KA+KH=AH\). A számolást egyszerűsíthetjük, ha az \(\displaystyle a\) oldalú négyzeteketre és a \(\displaystyle K\) pontra egy origó középpontú, \(\displaystyle \displaystyle{\lambda=\frac{1}{a}}\) arányú középpontos hasonlóságot alkalmazunk, ezzel a bizonyítandó állítás nem változik meg. A hasonlósággal a négyzeteket három, egységnyi oldalú négyzetbe visszük át, és így
| \(\displaystyle (1)\) | \(\displaystyle A(0;0),\quad B(1;0),\quad C(1;1),\quad D(0;1),\quad E(2;0),\quad F(2;1),\quad G(3;0),\quad H(3;1).\) |
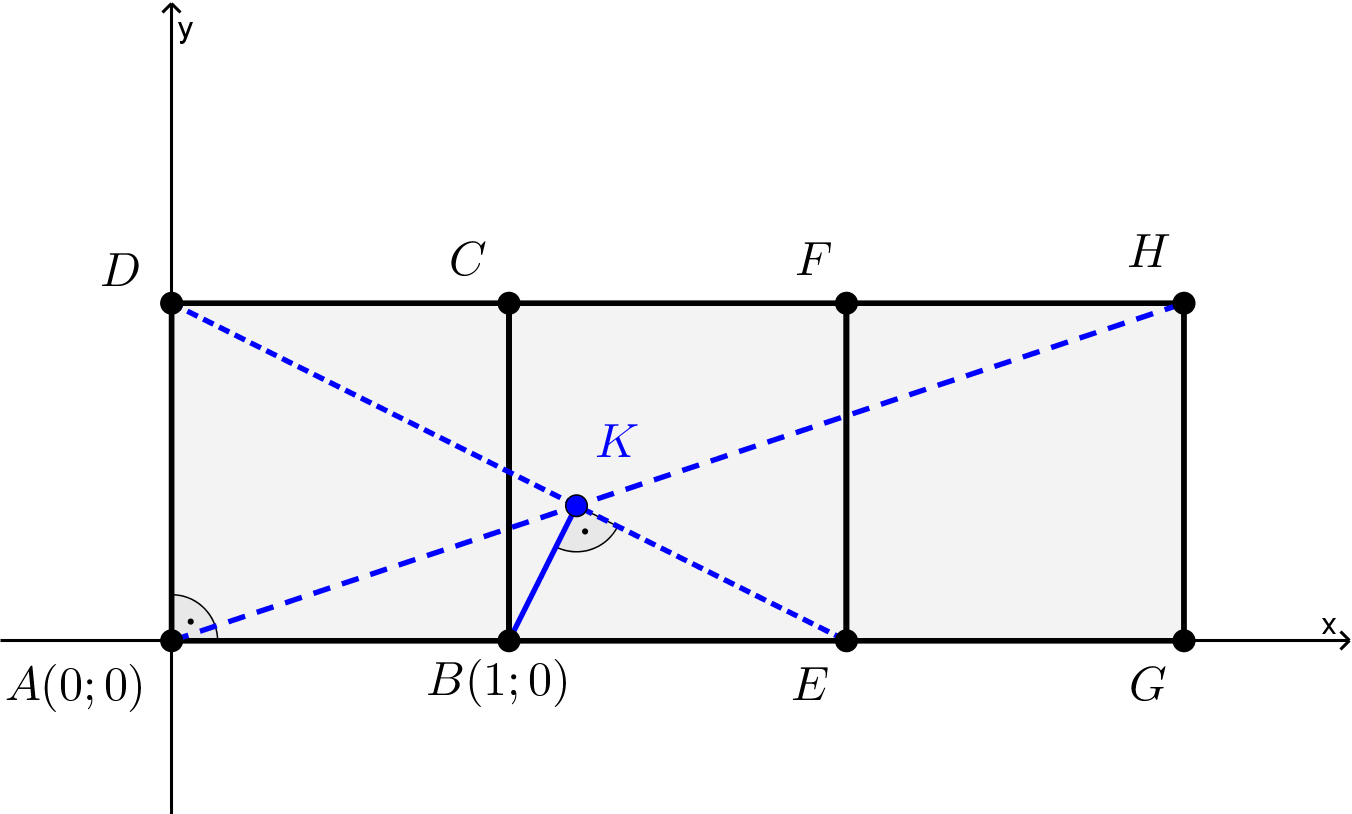
2. ábra
A \(\displaystyle DE\) egyenes meredeksége (1)-ből következően \(\displaystyle \displaystyle{-\frac{1}{2}}\), ezért az egyenes egyenlete
| \(\displaystyle (2)\) | \(\displaystyle y=-\frac{1}{2}x+1.\) |
A \(\displaystyle BK\) egyenes merőleges \(\displaystyle DE\)-re, tehát meredeksége \(\displaystyle m=2\), így a \(\displaystyle BK\) egyenes egyenlete \(\displaystyle y=2x+b\) alakú. Mivel ez az egyenes áthalad a \(\displaystyle B(1;0)\) ponton, a megfelelő koordináták behelyettesítésével kapjuk, hogy \(\displaystyle b=-2\), azaz a \(\displaystyle BK\) egyenes egyenlete
| \(\displaystyle (3)\) | \(\displaystyle y=2x-2.\) |
A (2) és (3) egyenletekből álló egyenletrendszer megoldása az
\(\displaystyle \displaystyle{x=\frac{6}{5};\quad y=\frac{2}{5}}\)
számpár, ezért a \(\displaystyle K\) pont koordinátái
| \(\displaystyle (4)\) | \(\displaystyle \displaystyle{K\Bigg(\frac{6}{5}; \frac{2}{5}\Bigg)}.\) |
Az (1) és (4) eredmények segítségével és a távolságképlet alkalmazásával azt kapjuk, hogy
| \(\displaystyle (5)\) | \(\displaystyle \displaystyle{KA=\frac{2\sqrt{10}}{5}; \quad KH=\frac{3\sqrt{10}}{5}; \quad AH=\sqrt{10}}.\) |
Az (5) összefüggés alapján egyszerű számolással láthatjuk be, hogy \(\displaystyle KA+KH=AH\) valóban teljesül.
Ha az \(\displaystyle A, K, H\) pontok nem lennének egy egyenesen, akkor háromszöget alkotnának, és akkor a háromszög-egyenlőtlenség miatt \(\displaystyle KA+KH=AH\) nem lehetne igaz.
Mivel pedig \(\displaystyle KA+KH=AH\) fennáll, ezért az \(\displaystyle A, K, H\) pontok egy egyenesen vannak.
3. megoldás. A feladat megoldásához elegendő igazolnunk, hogy \(\displaystyle AKH\sphericalangle=180^{\circ}\), ekkor teljesül, hogy az \(\displaystyle A, K, H\) pontok egy egyenesen vannak.
Tekintsük a feltételeknek megfelelően készített 3. ábrát, amelyen a három egymás mellé helyezett négyzetet tükröztük az \(\displaystyle AG\) egyenesre, az így létrejött három négyzetet pedig a négyzetek \(\displaystyle AG\)-vel párhuzamos oldalának egyenesére. Ezzel létrehoztunk egy kilenc egybevágó négyzetből álló nagyobb négyzetet.
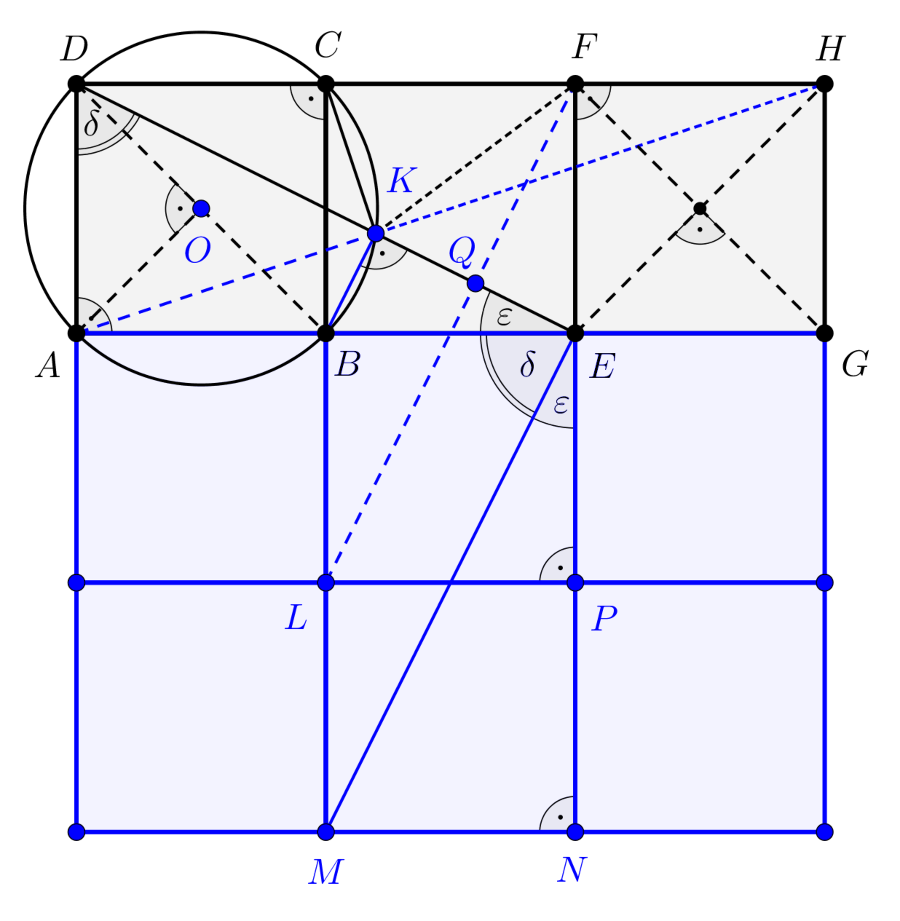
3. ábra
A \(\displaystyle BD\) szakasz az \(\displaystyle ABCD\) négyzet \(\displaystyle C\) csúcsából nyilvánvalóan derékszögben látszik, és a \(\displaystyle BD\) szakasznak a \(\displaystyle K\) pontból mért látószöge is \(\displaystyle 90^{\circ}\)-os a \(\displaystyle BK\perp{DE}\) feltétel miatt. Ezért a \(\displaystyle K\) pont illeszkedik az \(\displaystyle ABCD\) négyzet \(\displaystyle O\) középpontú körülírt körére.
Az \(\displaystyle O\) középpontból az \(\displaystyle ABCD\) négyzet oldalai derékszögben látszanak, így a kör kerületének \(\displaystyle K\) pontjából a középponti és kerületi szögek összefüggése szerint az oldalak látószöge \(\displaystyle 45^{\circ}\)-os. Eszerint
| \(\displaystyle (1)\) | \(\displaystyle AKB\sphericalangle=DKA\sphericalangle=CKD\sphericalangle=45^{\circ}.\) |
Azt fogjuk bizonyítani, hogy az \(\displaystyle EH\) szakasz a \(\displaystyle K\) pontból \(\displaystyle 45^{\circ}\)-os szögben látszik. Ez egyenértékű a feladat állításával, mert akkor
\(\displaystyle AKB\sphericalangle+BKE\sphericalangle+EKH\sphericalangle=45^{\circ}+90^{\circ}+45^{\circ}=180^{\circ}.\)
Az \(\displaystyle EDA\) háromszög \(\displaystyle E\), illetve \(\displaystyle D\) csúcsánál levő hegyesszögeit a 3. ábrán \(\displaystyle \displaystyle{\varepsilon}\)-nal, illetve \(\displaystyle \displaystyle{\delta}\)-val jelöltük, a két szög összegére nyilván
| \(\displaystyle (2)\) | \(\displaystyle \varepsilon+\delta=90^{\circ}\) |
teljesül.
Az \(\displaystyle EDA\), \(\displaystyle FLP\), \(\displaystyle EMN\) és \(\displaystyle MEB\) derékszögű háromszögek az oldalak páronkéni egyenlősége miatt egybevágók, ezért
| \(\displaystyle (3)\) | \(\displaystyle PFL\sphericalangle=NEM\sphericalangle=\varepsilon;\quad MEB\sphericalangle=\delta.\) |
A (2)-(3) eredmények alapján \(\displaystyle BMEK\) derékszögű trapéz.
Ugyanakkor az \(\displaystyle EFLM\) négyszög paralelogramma, mert az egyenlő hosszúságú \(\displaystyle EF\) és \(\displaystyle LM\) szakaszok párhuzamosak. Ebből az következik, hogy \(\displaystyle EM\parallel{FL}\), és mivel \(\displaystyle KE\perp{EM}\), ezért \(\displaystyle KE\perp{FL}\) is igaz.
Az \(\displaystyle L\) pont a \(\displaystyle BM\) szakasz felezőpontja, így \(\displaystyle KB\parallel{FL}\parallel{EM}\) miatt a \(\displaystyle BMEK\) derékszögű trapéz középvonalának egyenese éppen az \(\displaystyle FL\) egyenes, amely a \(\displaystyle KE\) szakaszt merőlegesen felezi a \(\displaystyle Q\) pontban.
Az is nyilvánvaló, hogy a \(\displaystyle EH\) szakasz felezőmerőlegese \(\displaystyle GF\), és az előzőek szerint a \(\displaystyle KE\) szakasz felezőmerőlegese \(\displaystyle QF\). Az \(\displaystyle EKH\) háromszög két oldalának felezőmerőlegesei a körülírt kör \(\displaystyle F\) középpontjában metszik egymást.
Az \(\displaystyle F\) pontból az \(\displaystyle EKH\) háromszög körülírt körének \(\displaystyle EH\) húrja \(\displaystyle 90^{\circ}\)-os szögben látszik, ennek a húrnak a \(\displaystyle K\) pontból mért látószöge a középponti és kerületi szögek összefüggéséből adódóan
\(\displaystyle EKH\sphericalangle=45^{\circ}.\)
Ezzel bizonyítottuk, hogy
\(\displaystyle AKB\sphericalangle+BKE\sphericalangle+EKH\sphericalangle=45^{\circ}+90^{\circ}+45^{\circ}=180^{\circ},\)
tehát az \(\displaystyle A, K, H\) pontok valóban egy egyenesen vannak.
Megjegyzések. 1) Ha az 1. megoldásban a \(\displaystyle K'\) pont bevezetése helyett a \(\displaystyle K\) pont koordinátáit számoltuk volna ki, akkor a 2. megoldásban leírtak szerint bizonyíthattuk volna, hogy \(\displaystyle KA+KH=AH\).
2) A 3. ábra segítségével igazolható, hogy \(\displaystyle CAK\) és \(\displaystyle CHK\) derékszögű háromszögek, amelyeknek derékszögű csúcsa éppen \(\displaystyle K\). A feladat állítása ebből is következik.
Statistics:
117 students sent a solution. 5 points: 91 students. 4 points: 4 students. 3 points: 2 students. 2 points: 1 student. 1 point: 5 students. 0 point: 3 students. Unfair, not evaluated: 5 solutionss.
Problems in Mathematics of KöMaL, February 2023
