 Problem C. 1758. (March 2023)
Problem C. 1758. (March 2023)
C. 1758. Adam found a magic square in a magazine. (A magic square is a \(\displaystyle 3\times3\) table of numbers in which the sum of the numbers is the same in all rows, columns and diagonals, see the figure.) He filled in the square correctly, and then selected a row or column at random. He wrote down the three numbers in the order as they appeared left to right or top down. These are the numbers \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\) in the equation \(\displaystyle ax^2 + bx + c = 0\). Adam was happy to observe that the resulting equation had two distinct real roots, and calculated the sum of the squares of the roots. What numbers may he have got as a result?
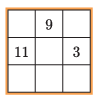
Proposed by O. Teleki, Tököl
(5 pont)
Deadline expired on April 11, 2023.
Sorry, the solution is available only in Hungarian. Google translation
1. megoldás. Először töltsük ki a bűvös négyzetet, jelöljük a középső mezőben lévő számot \(\displaystyle x\)-szel. Ekkor minden sorban, oszlopban és átlóban \(\displaystyle 14+x\) a számok összege, vagyis máris tudjuk, hogy az alsó középső mezőben az \(\displaystyle 5\)-ös áll. Ha a bal alsó mezőben lévő számot \(\displaystyle y\)-nal jelöljük, akkor a jobb felső mezőben a \(\displaystyle 14–y\) áll. Mivel az alsó sorban és a jobb oldali oszlopban azonos a számok összege, ezért \(\displaystyle y+5= (14–y)+3\). Ebből \(\displaystyle 2y=12\), tehát a bal alsó mezőben a \(\displaystyle 6\)-os szám áll. A jobb alsó mezőben ezek szerint \(\displaystyle 3+x\) van, így lesz az alsó sorban is \(\displaystyle 14+x\) a számok összege. Mivel a felső sorban és a bal felső–jobb alsó átlóban is ugyanannyi a számok összege, így \(\displaystyle 9+8=3+2x\). Ebből \(\displaystyle x=7\) – tehát ez van a középső mezőben – és így a bal felső mezőben a \(\displaystyle 4\), a jobb alsóban a \(\displaystyle 10\) áll. Immáron megvan a bűvös négyzet minden eleme:
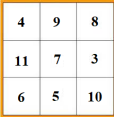
Még ellenőriznünk kell, hogy tényleg minden sorban és oszlopban ugyanannyi a számok összege, de valóban, mindenütt \(\displaystyle 21\)-et kapunk. A feladatban megadott feltételek alapján Ádám az alábbi \(\displaystyle 6\) másodfokú egyenletet egyikét írta fel:
\(\displaystyle 1)\) \(\displaystyle 4x^2 + 9x + 8 = 0\), amelynek diszkriminánsa \(\displaystyle D_1=9^2-4 \cdot 4 \cdot 8=-47\);
\(\displaystyle 2)\) \(\displaystyle 11x^2 + 7x + 3 = 0\), amelynek diszkriminánsa \(\displaystyle D_2=7^2-4 \cdot 11 \cdot 3=-83\);
\(\displaystyle 3)\) \(\displaystyle 6x^2 + 5x + 10 = 0\), amelynek diszkriminánsa \(\displaystyle D_3=5^2-4 \cdot 6 \cdot 10=-215\);
\(\displaystyle 4)\) \(\displaystyle 4x^2 + 11x + 6 = 0\), amelynek diszkriminánsa \(\displaystyle D_4=11^2-4 \cdot 4 \cdot 6=25\);
\(\displaystyle 5)\) \(\displaystyle 9x^2 + 7x + 5 = 0\), amelynek diszkriminánsa \(\displaystyle D_5=7^2 - 4 \cdot 9 \cdot 5=-131\);
\(\displaystyle 6)\) \(\displaystyle 8x^2 + 3x + 10 = 0\), amelynek diszkriminánsa \(\displaystyle D_6=3^2-4 \cdot 8 \cdot 10=-311\).
Láthatjuk, hogy kizárólag \(\displaystyle D_4 >0\), ezért Ádám biztosan a \(\displaystyle 4\)-es számú egyenletet írta fel. A megoldóképlettel kiszámíthatjuk a két valós gyököt, amelyek \(\displaystyle x_1=-\frac34\) és \(\displaystyle x_2=-2\). A gyökök négyzetösszege
\(\displaystyle x_1^2+x_2^2= (-\frac34)^2+(-2)^2=\frac{73}{16},\)
vagyis ha Ádám helyesen számolt, akkor \(\displaystyle \displaystyle{\frac{73}{16}}\)-ot kapott.
2. megoldás. Jelöljük a bűvös négyzet bal felső sarkában lévő számot \(\displaystyle a\)-val, a jobb felső sarokban lévőt \(\displaystyle b\)-vel, a négyzet közepén lévőt \(\displaystyle c\)-vel, az alsó sorban álló számokat pedig balról jobbra haladva, rendre \(\displaystyle d\)-vel, \(\displaystyle e\)-vel és \(\displaystyle f\)-fel. Mivel az egyes sorokban, oszlopokban és egy-egy átlóban található számok összege megegyezik, ezért speciálisan a középső sorban, illetve oszlopban álló számok összege egyenlő, azaz \(\displaystyle 11+c+3=9+c+e\), amelyből \(\displaystyle e=5\) adódik. Hasonlóképpen az első és harmadik sorban lévő számok összege megegyezik a két átlóban lévők összegével: \(\displaystyle a+9+b+d+5+f=a+c+f+b+c+d,\) ebből \(\displaystyle 2c=14\), vagyis \(\displaystyle c=7\), így az összeg minden esetben \(\displaystyle 21\) kell, hogy legyen.
A négyzet \(\displaystyle 2-2\) sarkában álló számok összegét kiszámíthatjuk a megfelelő sor, oszlop, vagy átló összegéből: \(\displaystyle a+b=21-9=12\), \(\displaystyle a+d=21-11=10\), \(\displaystyle a+f=14\) és \(\displaystyle b+d=14\). Az első két egyenlet megfelelő oldalait összeadva, majd kivonva az utolsó egyenlet megfelelő oldalait, azt kapjuk, hogy \(\displaystyle 2a=8\), amiből \(\displaystyle a=4\). Ezt rendre visszahelyettesítve az első, második és harmadik egyenletbe: \(\displaystyle b=12-4=8\), \(\displaystyle d=10-4=6\) és \(\displaystyle f=14-4=10\).
A fentiek alapján a bűvös négyzet kitöltése egyértelmű, ezért Ádám az alábbi ábrán látható módon töltötte azt ki.

A feladat feltételei alapján Ádám az alábbi \(\displaystyle 6\) másodfokú egyenlet egyikét írta fel:
\(\displaystyle 1)\) \(\displaystyle 4x^2 + 9x + 8 = 0\), amelynek diszkriminánsa \(\displaystyle D_1=9^2-4 \cdot 4 \cdot 8=-47\);
\(\displaystyle 2)\) \(\displaystyle 11x^2 + 7x + 3 = 0\), amelynek diszkriminánsa \(\displaystyle D_2=7^2-4 \cdot 11 \cdot 3=-83\);
\(\displaystyle 3)\) \(\displaystyle 6x^2 + 5x + 10 = 0\), amelynek diszkriminánsa \(\displaystyle D_3=5^2-4 \cdot 6 \cdot 10=-215\);
\(\displaystyle 4)\) \(\displaystyle 4x^2 + 11x + 6 = 0\), amelynek diszkriminánsa \(\displaystyle D_4=11^2-4 \cdot 4 \cdot 6=25\);
\(\displaystyle 5)\) \(\displaystyle 9x^2 + 7x + 5 = 0\), amelynek diszkriminánsa \(\displaystyle D_5=7^2 - 4 \cdot 9 \cdot 5=-131\);
\(\displaystyle 6)\) \(\displaystyle 8x^2 + 3x + 10 = 0\), amelynek diszkriminánsa \(\displaystyle D_6=3^2-4 \cdot 8 \cdot 10=-311\).
Láthatjuk, hogy kizárólag \(\displaystyle D_4 >0\), ezért Ádám biztosan a \(\displaystyle 4\)-es számú egyenletet írta fel. A két különböző valós gyök négyzetösszegének kiszámításakor alkalmazhatjuk a Viéte-formulákat:
\(\displaystyle x_1^2+x_2^2=(x_1+x_2)^2-2x_1x_2=\Big(-\frac{11}{4} \Big)^2-2 \cdot \frac{6}{4}=\frac{73}{16}(=4,\!5625).\)
Ha Ádám helyesen számolt, akkor a \(\displaystyle \displaystyle{\frac{73}{16}}\)-ot kapta a gyökök négyzetösszegeként.
Statistics:
115 students sent a solution. 5 points: 64 students. 4 points: 17 students. 3 points: 12 students. 2 points: 8 students. 1 point: 1 student. 0 point: 1 student. Unfair, not evaluated: 5 solutionss.
Problems in Mathematics of KöMaL, March 2023
