 Problem C. 1782. (October 2023)
Problem C. 1782. (October 2023)
C. 1782. From vertex \(\displaystyle D\) of a square \(\displaystyle ABCD\), a tangent is drawn to the semicircle of diameter \(\displaystyle AB\) lying inside the square. The point of tangency (different from point \(\displaystyle A\)) is \(\displaystyle E\), and the midpoint of line segment \(\displaystyle AB\) is \(\displaystyle F\). The tangent intersects line \(\displaystyle BC\) at point \(\displaystyle G\) and line \(\displaystyle AB\) at point \(\displaystyle H\). Line \(\displaystyle EF\) intersects line \(\displaystyle DA\) at point \(\displaystyle K\). Prove that the radii of the inscribed circles of triangles \(\displaystyle FHE\), \(\displaystyle DGC\) and \(\displaystyle DKE\), in this order, form three consecutive terms of an increasing arithmetric sequence.
Proposed by B. Bíró, Eger
(5 pont)
Deadline expired on November 10, 2023.
Sorry, the solution is available only in Hungarian. Google translation
I. megoldás A megoldás során fel fogjuk használni azt az ismert összefüggést, hogy ha egy derékszögű háromszög befogói \(\displaystyle a\) és \(\displaystyle b\), átfogója \(\displaystyle c\), akkor beírt körének sugara
| \(\displaystyle (1)\) | \(\displaystyle \displaystyle{r=\frac{a+b-c}{2}}.\) |
Tekintsük a következő ábrát, amelyen a négyzet oldalának hosszát \(\displaystyle a\)-val jelöltük.
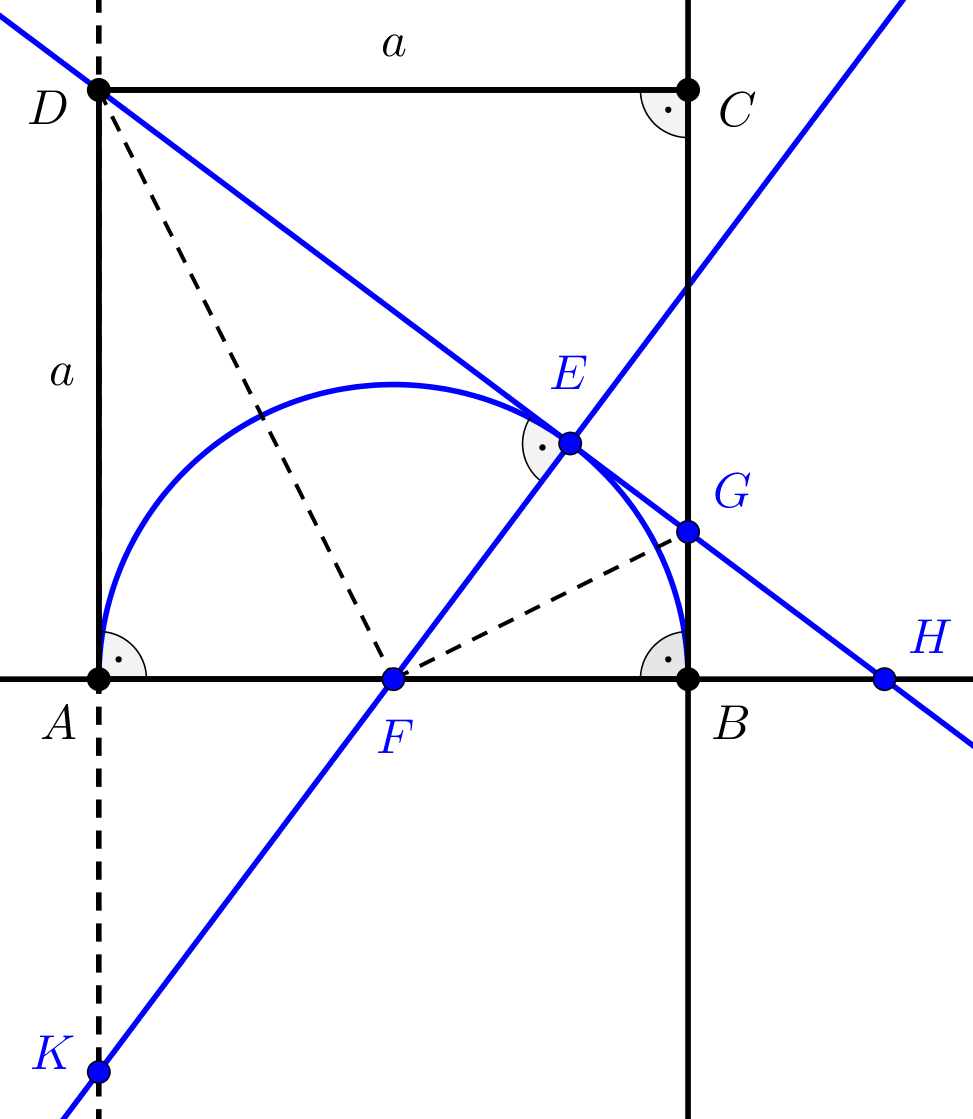
A \(\displaystyle DE\) érintő merőleges a félkör középpontjából az érintési pontba húzott sugárra, ezért \(\displaystyle DE\perp FE\), vagyis az \(\displaystyle FHE\), \(\displaystyle DGC\) és \(\displaystyle DKE\) háromszögek mindegyike derékszögű. Másrészt pedig \(\displaystyle \displaystyle{FA=FB=FE=\frac{a}{2}}\) és az érintőszakaszok hosszának egyenlősége miatt \(\displaystyle DA=DE=a\).
Ezek alapján kiszámítjuk az \(\displaystyle FHE\), \(\displaystyle DGC\), \(\displaystyle DKE\) derékszögű háromszögek oldalainak hosszát.
Az \(\displaystyle FDA\) és \(\displaystyle FDE\) derékszögű háromszögek a megfelelő oldalak hosszának egyenlősége miatt egybevágók. A \(\displaystyle GE\) és \(\displaystyle GB\) a félkörhöz húzott érintőszakaszok, az \(\displaystyle FGE\) és \(\displaystyle FGB\) derékszögű háromszögek megfelelő oldalainak hossza is egyenlő, tehát ezek a háromszögek is egybevágók. Az egybevágó háromszögek megfelelő szögei egyenlők, így \(\displaystyle FD\) felezi az \(\displaystyle AFE \sphericalangle\)-et, \(\displaystyle FG\) pedig felezi a \(\displaystyle BFE \sphericalangle\)-et. Ezt azt jelenti, hogy \(\displaystyle DFG\sphericalangle=90^{\circ}\). A \(\displaystyle DGF\) derékszögű háromszögben alkalmazhatjuk a magasságtételt, eszerint \(\displaystyle FE=\sqrt{DE\cdot GE}\), azaz \(\displaystyle \displaystyle{\frac{a}{2}=\sqrt{a\cdot GE}}\), ahonnan a műveletek elvégzésével és egyszerűsítéssel kapjuk, hogy
| \(\displaystyle (2)\) | \(\displaystyle \displaystyle{GE=GB=\frac{a}{4}}.\) |
A \(\displaystyle HGB\) és \(\displaystyle HDA\) derékszögű háromszögek megfelelő szögei egyenlők, ezért a két háromszög hasonló, a hasonlóság aránya (2) alapján \(\displaystyle \displaystyle{\frac{1}{4}}\), így
\(\displaystyle \displaystyle{\frac{BH}{BH+a}=\frac{1}{4}},\)
ebből egyszerű számolással adódik, hogy
| \(\displaystyle (3)\) | \(\displaystyle \displaystyle{BH=\frac{a}{3}},\) |
innen pedig (például a \(\displaystyle HGB\) háromszögre felírt Pitagorasz-tétel segítségével) kapjuk, hogy
| \(\displaystyle (4)\) | \(\displaystyle \displaystyle{HG=\frac{5a}{12}}.\) |
Az \(\displaystyle FHE\) derékszögű háromszög befogói és átfogója tehát a (2)–(3)–(4) összefüggések segítségével:
\(\displaystyle \displaystyle{FE=\frac{a}{2}=\frac{6a}{12}; \qquad EH=GE+HG=\frac{a}{4}+\frac{5a}{12}=\frac{8a}{12};\qquad FH=FB+BH=\frac{a}{2}+\frac{a}{3}=\frac{10a}{12}}.\)
Alkalmazzuk az (1) tételt az \(\displaystyle FHE\) derékszögű háromszögre, ahonnan egyszerű számolás után:
| \(\displaystyle (5)\) | \(\displaystyle \displaystyle{r_{FHE}=\frac{2a}{12}}.\) |
Felhasználjuk (2)-t és azt, hogy \(\displaystyle DE=a\), ezzel a \(\displaystyle DGC\) derékszögű háromszög befogóinak és átfogójának hossza:
\(\displaystyle \displaystyle{CD=a=\frac{12a}{12}; \qquad CG=a-GB=\frac{3a}{4}=\frac{9a}{12};\qquad DG=DE+GE=a+\frac{a}{4}=\frac{15a}{12}},\)
ezek alapján az (1) tételből
| \(\displaystyle (6)\) | \(\displaystyle \displaystyle{r_{DGC}=\frac{3a}{12}}\) |
következik.
Az \(\displaystyle FKA\) és \(\displaystyle FHE\) derékszögű háromszögek közös \(\displaystyle F\) csúcsánál levő belső szögei csúcsszögek, tehát egyenlő nagyságúak, ezért a két háromszög másik hegyesszöge is egyenlő, így a háromszögek hasonlók, de mivel a megfelelő \(\displaystyle FA\) és \(\displaystyle FE\) befogók hossza egyaránt \(\displaystyle \displaystyle{\frac{a}{2}}\), ezért a két háromszög egybevágó. Ez azt jelenti, hogy
\(\displaystyle \displaystyle{AK=EH=\frac{8a}{12}};\qquad FK=FH=\frac{10a}{12},\)
ezért a \(\displaystyle DKE\) derékszögű háromszög befogói és átfogója:
\(\displaystyle \displaystyle{DE=a=\frac{12a}{12}; \qquad KE=\frac{a}{2}+FK=\frac{16a}{12};\qquad DK=a+AK=\frac{20a}{12}},\)
így tehát (1) szerint
| \(\displaystyle (7)\) | \(\displaystyle \displaystyle{r_{DKE}=\frac{4a}{12}}.\) |
Az (5)–(6)–(7) egyenlőségek igazolják a feladat állítását, amely szerint az \(\displaystyle FHE\), \(\displaystyle DGC\) és \(\displaystyle DKE\) háromszögek beírt köreinek sugarai ebben a sorrendben egy növekvő számtani sorozat közvetlen egymás utáni tagjai, a számtani sorozat különbsége pontosan a négyzet oldalhosszának \(\displaystyle \displaystyle{12}\)-ed része. Ezzel a megoldást befejeztük.
II. megoldás Használjuk az I. megoldás-hoz készített ábrát. Megállapításaink a (2)-vel jelzett összefüggésig megegyeznek az előző megoldással.
Legyen most \(\displaystyle ADE\sphericalangle=\alpha\), ekkor könnyen látható, hogy \(\displaystyle FHE\sphericalangle=EDC\sphericalangle=DKE\sphericalangle=90^{\circ}-\alpha\), továbbá \(\displaystyle DGC\sphericalangle=HFE\sphericalangle=\alpha\).
Mindezekből az következik, hogy az alábbi derékszögű háromszögek páronként hasonlók:
\(\displaystyle FHE \sim GDC \sim DKE.\)
Jelöljük az \(\displaystyle FHE\) beírt körének sugarát \(\displaystyle r\)-rel.
Ekkor az \(\displaystyle FHE\)-t a \(\displaystyle GDC\)-be képező hasonlóság aránya alapján megkaphatjuk a \(\displaystyle GDC\) beírt körének sugarát. Az arány a két derékszögű háromszög megfelelő oldalainak arányával, ebben az esetben a \(\displaystyle 90^{\circ}-\alpha\) szöggel szemközti befogók arányával egyenlő:
\(\displaystyle \displaystyle{\frac{CG}{FE}=\frac{a-\frac{1}{4}a}{\frac{a}{2}}=\frac{\frac{3}{4}a}{\frac{a}{2}}=\frac{3}{2}}.\)
Ezért a \(\displaystyle GDC\) háromszög beírt körének sugara \(\displaystyle \displaystyle{\frac{3}{2}r}\).
Hasonlóképpen belátható, hogy a \(\displaystyle GDC\) háromszöget a \(\displaystyle DKE\) háromszögbe képező hasonlóság aránya
\(\displaystyle \displaystyle{\frac{CG}{DE}=\frac{a}{\frac{3}{4}a}=\frac{4}{3}},\)
így a \(\displaystyle DKE\) beírt körének sugara a \(\displaystyle GDC\)-be írt kör sugarának \(\displaystyle \displaystyle{\frac{4}{3}}\)-a, vagyis \(\displaystyle \displaystyle{\frac{3}{2}r\cdot \frac{4}{3}=2r}\).
A három sugár tehát rendre
\(\displaystyle \displaystyle{r,\qquad \frac{3}{2}r,\qquad 2r}.\)
Ezek valóban egy számtani sorozat egymást követő tagjai.
Megjegyzés. Könnyen belátható, hogy a II. megoldás-ban kapott \(\displaystyle \displaystyle{d=\frac{r}{2}}\) érték az \(\displaystyle ABCD\) négyzet oldalhosszának \(\displaystyle 12\)-ed része, azaz \(\displaystyle \displaystyle{\frac{r}{2}=\frac{a}{12}}\), és ezért \(\displaystyle \displaystyle{r=\frac{a}{6}}\).
Statistics:
65 students sent a solution. 5 points: Baksa Anna, Baumgartner Ádám, Bencze Mátyás, Braun Zsófia, Dancsák Dénes, Fiser 234 Boldizsár, Gál András, Gombos Dániel , Gyuricsek Ákos, Han Xinzhi, Inokai Ádám, Iván Máté Domonkos, Járdánházi-Kurutz Vilmos, Márfai Dóra, Masa Barnabás, Medgyesi Júlia, Nagy 292 Korina, Németh Hanna Júlia , Seprődi Barnabás Bendegúz, Szabó Donát, Telkes Ágota, Török Eszter Júlia, Volford Barnabás, Žigo Boglárka. 4 points: Alexandrova Angelina, Balogh Péter, Barna Márton, Bérczes Botond, Bettesch Emma Léda, Ehrlich Máté, Károlyi József, Papp Zsófia, Petró Péter, Simon Bálint. 3 points: 6 students. 2 points: 9 students. 1 point: 5 students. 0 point: 3 students.
Problems in Mathematics of KöMaL, October 2023
