 Problem C. 1789. (December 2023)
Problem C. 1789. (December 2023)
C. 1789. A tortoise travelled a distance of \(\displaystyle 14\) units in the plane. Each of its steps were of a unit's length. After each step it made a turn: if the number of the previous step was odd, then with an angle of \(\displaystyle 60^{\circ}\), if even, then with an angle of \(\displaystyle 90^{\circ}\). In steps \(\displaystyle 3\), \(\displaystyle 5\), \(\displaystyle 8\) and \(\displaystyle 12\) he turned to the right, in the remaining steps he turned to the left.
\(\displaystyle a)\) Prove that the tortoise will end up in its initial position facing in its initial direction after its \(\displaystyle 14^{\text{th}}\) step.
\(\displaystyle b)\) Find the area enclosed by the walk of tortoise in algebraic form.
Submitted by Lajos Szilassi, Szeged
(5 pont)
Deadline expired on January 10, 2024.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Az a) feladatrész megoldásához ábrát készítünk. Ezen legyen a teknőc útvonalának kezdőpontja \(\displaystyle A\), az útvonal további pontjait jelöljük rendre a \(\displaystyle B\), \(\displaystyle C\), \(\displaystyle D\), \(\displaystyle E\), \(\displaystyle F\), \(\displaystyle G\), \(\displaystyle H\), \(\displaystyle I\), \(\displaystyle J\), \(\displaystyle K\), \(\displaystyle L\), \(\displaystyle M\), \(\displaystyle N\) betűkkel, a teknőc egy-egy lépését pedig egy-egy megfelelő egységvektorral. Az óramutató járásával ellentétes irányú (balra történő) elfordulások szögeit pozitív előjellel ellátva az óramutató járásával megegyező (jobbra történő) elfordulások szöge negatív lesz.
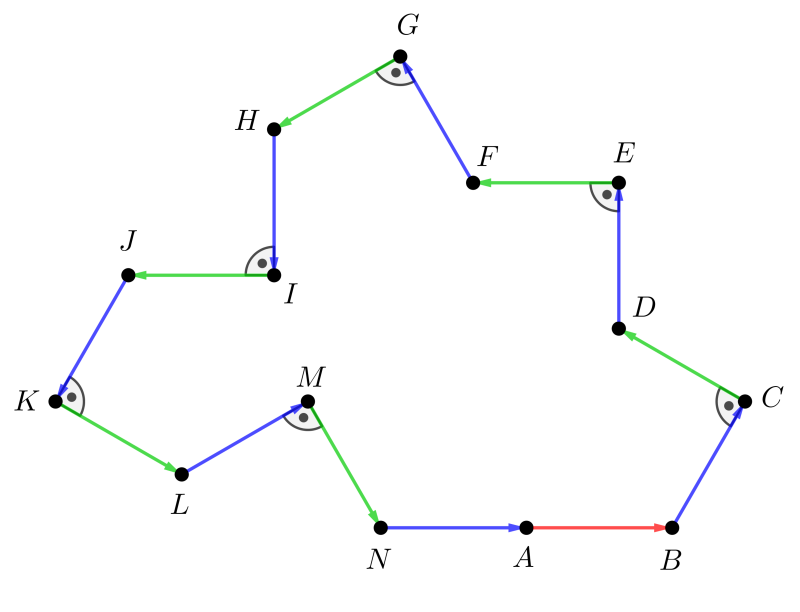
1. ábra
Egyszerű számolással igazolhatjuk, hogy a szögelfordulások előjeles összege \(\displaystyle 360^{\circ}\), ez pontosan azt jelenti, hogy az első és az utolsó egységvektor egyirányú.
Az utolsó egységvektor kezdőpontja \(\displaystyle N\), igazolni fogjuk, hogy a végpontja éppen \(\displaystyle A\). Egyszerűen látható, hogy minden egységvektornak az ellentett vektora is szerepel az ábrán.
Ezek a vektorpárok:
\(\displaystyle \overrightarrow{AB},\qquad \overrightarrow{EF};\)
\(\displaystyle \overrightarrow{BC},\qquad \overrightarrow{JK};\)
\(\displaystyle \overrightarrow{CD},\qquad \overrightarrow{KL};\)
\(\displaystyle \overrightarrow{DE},\qquad \overrightarrow{HI};\)
\(\displaystyle \overrightarrow{FG},\qquad \overrightarrow{MN};\)
\(\displaystyle \overrightarrow{GH},\qquad \overrightarrow{LM};\)
végül pedig az \(\displaystyle \overrightarrow{IJ}\) egységvektor ellentett vektora éppen az \(\displaystyle N\) kezdőpontú egységvektor. Eszerint a teknőc lépéseinek megfelelő egységvektorok összege nullvektor, ami csakis úgy lehetséges, hogy az utolsó egységvektor végpontja az \(\displaystyle A\) pont.
b) A teknőc lépéseivel az 1. ábra szerint egy zárt sokszöget járt körbe. A zárt sokszög területének kiszámításához átalakítjuk az előző ábrát: a sokszögből levágjuk a \(\displaystyle BCD\), \(\displaystyle DEF\), \(\displaystyle FGH\), \(\displaystyle JKL\) egyenlő szárú derékszögű háromszögeket és azok közül kettőt a \(\displaystyle HIJ\), \(\displaystyle LMN\) egyenlő szárú derékszögű háromszögek helyére illesztünk, a maradék kettőt pedig befogóikkal az \(\displaystyle NA\), illetve \(\displaystyle AB\) szakaszokra, úgy, hogy az így létrejövő \(\displaystyle P\) pont a zárt sokszög külső pontja legyen. Végül a \(\displaystyle P\) pontot \(\displaystyle NB\)-re tükrözve a \(\displaystyle Q\) pontot kapjuk.
Tekintsük az így készített ábrát.
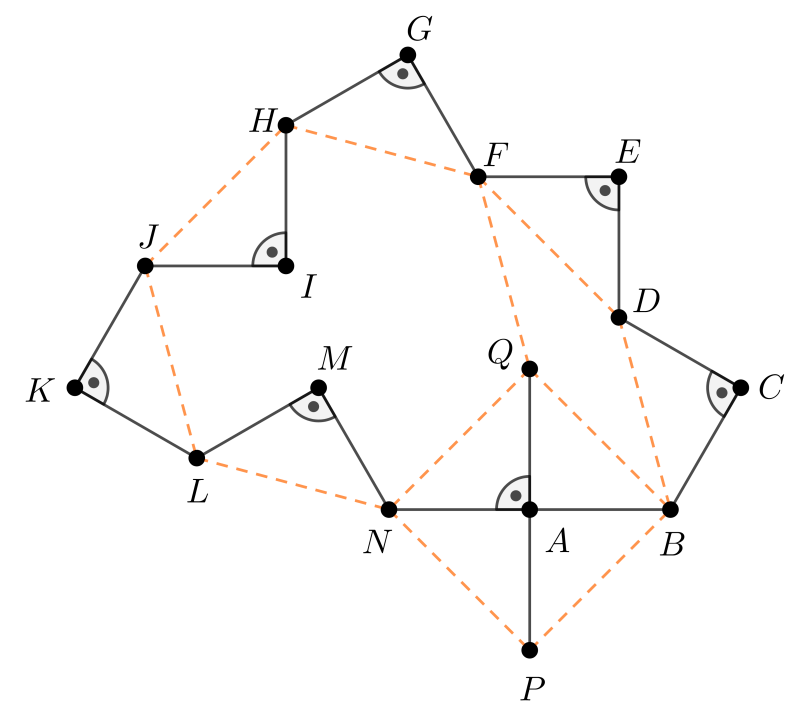
2. ábra
Az előző műveletek eredényeképpen a teknőc lépéseivel körbezárt sokszög területe a \(\displaystyle QFHJLN\) hatszög, a \(\displaystyle BDFQ\) és az \(\displaystyle NPBQ\) négyszög területének összegével egyenlő.
A hatszög oldalai egyenlő hosszúak, hiszen minden oldalhossza \(\displaystyle \sqrt{2}\)-vel egyenlő, a teknőc elfordulási szögei miatt a hatszög minden szöge \(\displaystyle 120^{\circ}\)-os, tehát \(\displaystyle QFHJLN\) szabályos hatszög, ezért területe
| \(\displaystyle (1)\) | \(\displaystyle \displaystyle{T_{QFHJLN}=6\cdot \frac{\big(\sqrt{2}\big)^2\cdot \sqrt{3}}{4}=3\cdot \sqrt{3}}.\) |
Az \(\displaystyle NPBQ\) négyszög négyzet, hiszen oldalaira teljesül, hogy \(\displaystyle NP=PB=BQ=QN=\sqrt{2}\), illetve \(\displaystyle QNP\sphericalangle=90^{\circ}\), ezért a területe
| \(\displaystyle (2)\) | \(\displaystyle \displaystyle{T_{NPBQ}=\big(\sqrt{2}\big)^2=2}.\) |
Végül \(\displaystyle BD=DF=FQ=QB=\sqrt{2}\), és a teknőc szögelfordulásaiból láthatóan a \(\displaystyle BDFQ\) négyszög szögei a \(\displaystyle B\), \(\displaystyle F\) csúcsoknál \(\displaystyle 30^{\circ}\)-osak, a \(\displaystyle D\), \(\displaystyle Q\) csúcsoknál \(\displaystyle 150^{\circ}\)-osak, így a négyszög rombusz, területe pedig
| \(\displaystyle (3)\) | \(\displaystyle \displaystyle{T_{BDFQ}=\sqrt{2}\cdot \sqrt{2}\cdot \sin 30^{\circ}=1}.\) |
A teknőc által körüljárt terület nagysága (1)-(2)-(3) alapján tehát:
\(\displaystyle T_{QFHJLN}+T_{NPBQ}+T_{BDFQ}=3\cdot \sqrt{3}+3.\)
Statistics:
143 students sent a solution. 5 points: Auer Sára, Balogh Péter, Barna Márton, Beinschroth Máté, Blaskovics Ádám, Blaskovics Bálint, Danka Emma, Gyuricsek Ákos, Inokai Ádám, Iván Máté Domonkos, Komlósdi Sára, Márfai Dóra, Masa Barnabás, Mikó Hédi Irma, Molnár-Sáska Tamás, Monoczki Máté, Pánovics Máté, Pázmándi Renáta , Petró Péter, Sebők Violetta Írisz, Sipos Márton, Szabó 926 Bálint, Szabó 926 Bence, Szabó Donát, Tóth 207 Bence, Török Eszter Júlia, Ujpál Bálint, Volford Barnabás, Wodala Gréta Klára, Žigo Boglárka, Zólyomi Csongor. 4 points: Aaishipragya Kahaly, Baksa Anna, Bencze Mátyás, Bérczes Botond, Budai Máté, Csáki Botond Benjámin, Domján István, Harmincz Sára, Hauser Márton, Károlyi József, Máté Kristóf, Németh Hanna Júlia , Válek Péter. 3 points: 4 students. 2 points: 34 students. 1 point: 20 students. 0 point: 22 students. Not shown because of missing birth date or parental permission: 8 solutions.
Problems in Mathematics of KöMaL, December 2023
