 Problem C. 1802. (February 2024)
Problem C. 1802. (February 2024)
C. 1802. In regular hexagon \(\displaystyle ABCDEF\) point \(\displaystyle M\) is chosen on diagonal \(\displaystyle AC\) and point \(\displaystyle N\) is chosen on diagonal \(\displaystyle DE\) satisfying \(\displaystyle \frac{AM}{AC}=\frac{CN}{CE}=k\). For which values of \(\displaystyle k\) will points \(\displaystyle B\), \(\displaystyle M\) and \(\displaystyle N\) be collinear?
Matlap, Kolozsvár (2017)
(5 pont)
Deadline expired on March 11, 2024.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Mivel \(\displaystyle M\), illetve \(\displaystyle N\) az \(\displaystyle AC\), illetve \(\displaystyle CE\) szakasz belső pontja, ezért \(\displaystyle k>0\), másrészt pedig \(\displaystyle AM<AC\), illetve \(\displaystyle CN<CE\) miatt \(\displaystyle k<1\), így
| \(\displaystyle (1)\) | \(\displaystyle 0<k<1.\) |
Legyen az \(\displaystyle ABCDEF\) szabályos hatszög oldala egységnyi, körülírt körének középpontját jelöljük \(\displaystyle O\)-val. Rajzoljuk meg a következő ábrán a \(\displaystyle \overrightarrow{BA}\) és \(\displaystyle \overrightarrow{BC}\) egységvektorokat, továbbá a \(\displaystyle \overrightarrow{BE}\), \(\displaystyle \overrightarrow{BM}\) és \(\displaystyle \overrightarrow{BN}\) vektorokat.
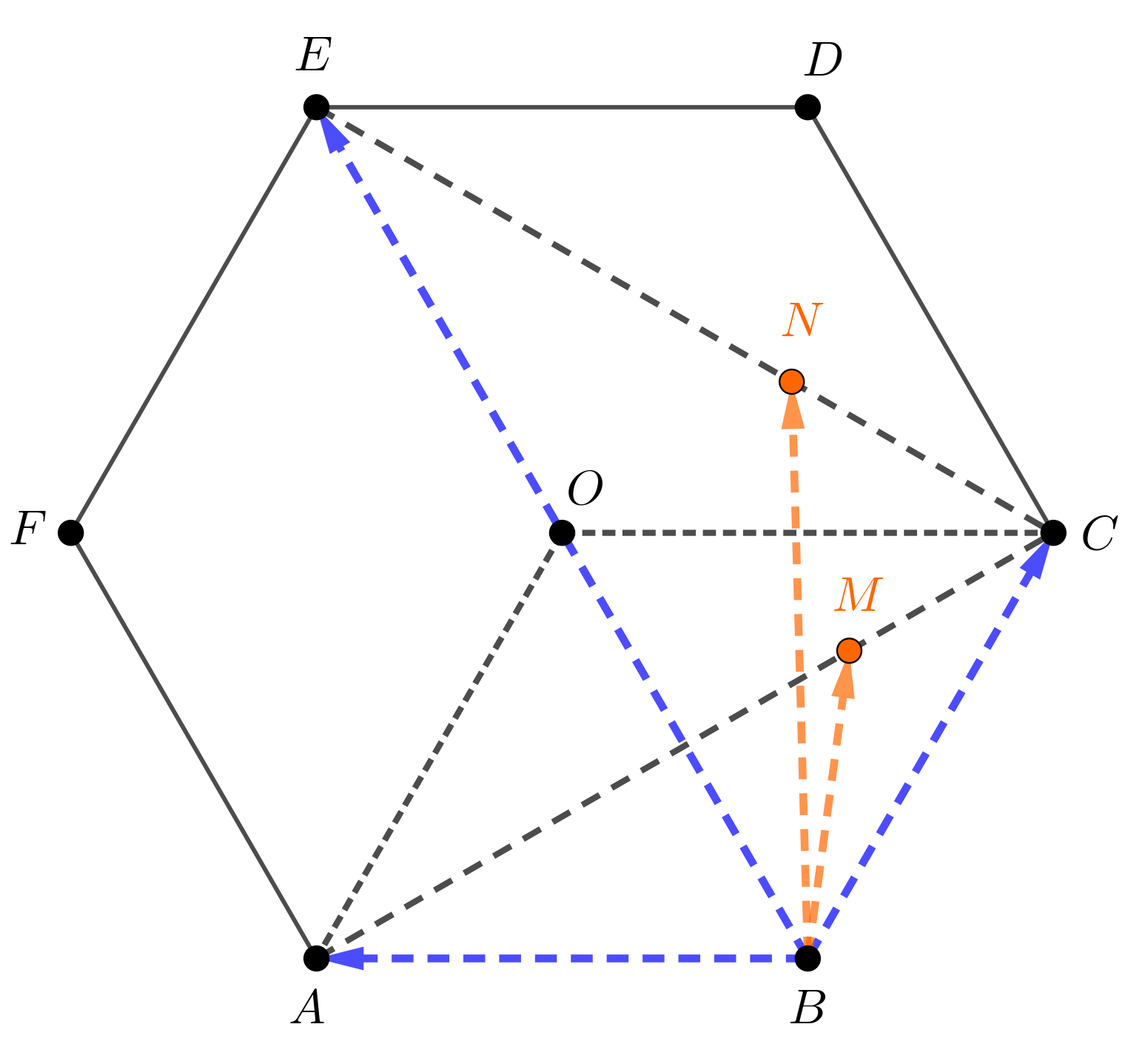
A \(\displaystyle \overrightarrow{BA}\) és \(\displaystyle \overrightarrow{BC}\) egységvektorokat bázisvektoroknak tekinthetjük, ezért a hatszög síkjában bármely vektor felírható mint \(\displaystyle \overrightarrow{BA}\) és \(\displaystyle \overrightarrow{BC}\) lineáris kombinációja.
A hatszög szimmetriatulajdonságai miatt a \(\displaystyle BE\) szakasz felezőpontja \(\displaystyle O\), ezért egyrészt \(\displaystyle \overrightarrow{BE}=2\overrightarrow{BO}\), másrészt az \(\displaystyle ABCO\) rombuszban \(\displaystyle \overrightarrow{BA}+\overrightarrow{BC}=\overrightarrow{BO}\), így
| \(\displaystyle (2)\) | \(\displaystyle \overrightarrow{BE}=2\Big(\overrightarrow{BA}+\overrightarrow{BC}\Big).\) |
A vektorösszeadás tulajdonságai miatt \(\displaystyle \overrightarrow{BM}=\overrightarrow{BA}+\overrightarrow{AM}\), ugyanakkor \(\displaystyle \displaystyle{\overrightarrow{AM}=\frac{AM}{AC}\cdot\Big(\overrightarrow{BC}-\overrightarrow{BA}\Big)}\), ezért \(\displaystyle \displaystyle{\overrightarrow{AM}=k\cdot\Big(\overrightarrow{BC}-\overrightarrow{BA}\Big)}\), ebből \(\displaystyle \overrightarrow{BM}=\overrightarrow{BA}+\overrightarrow{AM}\) alapján azt kapjuk, hogy
| \(\displaystyle (3)\) | \(\displaystyle \displaystyle{\overrightarrow{BM}=\Big(1-k\Big)\cdot\overrightarrow{BA}+k\cdot \overrightarrow{BC}}.\) |
Hasonlóképpen adódik \(\displaystyle \overrightarrow{BN}=\overrightarrow{BC}+\overrightarrow{CN}\) és \(\displaystyle \displaystyle{\overrightarrow{CN}=\frac{CN}{CE}\cdot\Big(\overrightarrow{BE}-\overrightarrow{BC}\Big)=k\cdot \Big(\overrightarrow{BE}-\overrightarrow{BC}\Big)}\), tehát
\(\displaystyle \overrightarrow{BN}=k\cdot \overrightarrow{BE}+(1-k)\cdot \overrightarrow{BC},\)
és így (2) alapján
| \(\displaystyle (4)\) | \(\displaystyle \overrightarrow{BN}=2k\cdot \overrightarrow{BA}+\Big(1+k\Big)\cdot\overrightarrow{BC}.\) |
A lineáris kombinációk (3) és (4) szerinti előállítása megadja a \(\displaystyle \overrightarrow{BM}\) és \(\displaystyle \overrightarrow{BN}\) vektoroknak a \(\displaystyle \overrightarrow{BA}\) és \(\displaystyle \overrightarrow{BC}\) alapvektorokra vonatkozó koordinátáit, ezek
\(\displaystyle \overrightarrow{BM}\Big(1-k;\quad k\Bigg),\)
és
\(\displaystyle \overrightarrow{BN}\Big(2k;\quad1+k\Bigg).\)
A \(\displaystyle B\), \(\displaystyle M\) és \(\displaystyle N\) pontok pontosan akkor lesznek kollineárisak, ha a \(\displaystyle \overrightarrow{BM}\) és \(\displaystyle \overrightarrow{BN}\) vektorok egyirányúak, vagy ellentétes irányúak.
Utóbbi eset a feltételek miatt nem fordulhat elő, mert az \(\displaystyle M\) és \(\displaystyle N\) pont is az \(\displaystyle ABC\sphericalangle\) szögtartományban van. Ezért \(\displaystyle \overrightarrow{BM}\) és \(\displaystyle \overrightarrow{BN}\) csak egyirányúak lehetnek. Ez azonban azt jelenti, hogy megfelelő koordinátáik aránya egyenlő, azaz
| \(\displaystyle (5)\) | \(\displaystyle \displaystyle{\frac{1-k}{2k}=\frac{k}{1+k}}.\) |
Az (5) egyenletből a műveletek elvégzése után \(\displaystyle \displaystyle{k^2=\frac{1}{3}}\), ahonnan a \(\displaystyle k\)-ra vonatkozó (1) feltételek miatt
\(\displaystyle \displaystyle{k=\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}}\)
következik. A feladatban szereplő \(\displaystyle B\), \(\displaystyle M\) és \(\displaystyle N\) pontok tehát pontosan akkor kollineárisak, ha \(\displaystyle \displaystyle{k=\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}}\).
Megjegyzések. 1) A feladat megoldása a (3) és (4) összefüggések után így is folytatható: a \(\displaystyle B, M, N\) pontok akkor és csak akkor kollineárisak, ha van olyan \(\displaystyle \lambda \in R\) szám, hogy \(\displaystyle \overrightarrow{BN}=\lambda\cdot \overrightarrow{BM}\). Ekkor
\(\displaystyle 2k\cdot \overrightarrow{BA}+(1+k\Big)\cdot\overrightarrow{BC}=\lambda\cdot\Big(\displaystyle{\Big(1-k\Big)\cdot\overrightarrow{BA}+k\cdot \overrightarrow{BC}\Big)}.\)
Innen rendezés után kapjuk, hogy
\(\displaystyle \big(2k-\lambda+\lambda\cdot k\big)\cdot\overrightarrow{BA}+\big(1+k-\lambda\cdot k\big)\cdot\overrightarrow{BC}=\overrightarrow{0}.\)
Mivel \(\displaystyle \overrightarrow{BA}\) és \(\displaystyle \overrightarrow{BC}\) egyike sem nullvektor, a vektorok egyenesei a feltétel miatt metsző egyenesek, ezért a kapott eredmény csak úgy állhat fenn, ha
\(\displaystyle 2k-\lambda+\lambda\cdot k=0,\)
és
\(\displaystyle 1+k-\lambda\cdot k=0.\)
A két egyenlet összeadása és rendezés után \(\displaystyle \lambda=3k+1\), ezt visszahelyettesítve, a műveletek elvégzésével és rendezéssel kapjuk, hogy \(\displaystyle 3k^2=1\), ahonnan a megoldásban látott módon \(\displaystyle \displaystyle{k=\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}}\) következik.
2) A feladat megoldható a komplex számsíkon is. Ehhez érdemes lehet tanulmányozni Reiman István: Geometriai feladatok megoldása a komplex számsíkon című szakköri füzetét, illetve Kiss Géza: Geometriai feladatok megoldása a komplex számsíkon című cikkét.
Statistics:
42 students sent a solution. 5 points: Balogh Péter, Barna Márton, Bencze Mátyás, Biborka Bernadett, Braun Zsófia, Gyuricsek Ákos, Harmincz Sára, Inokai Ádám, Iván Máté Domonkos, Nagy 292 Korina, Németh Hanna Júlia , Papp Zsófia, Petró Péter, Sebők Violetta Írisz, Simon Bálint, Szabó Donát, Török Eszter Júlia, Viczián Márk, Žigo Boglárka. 4 points: Baksa Anna, Csiszár András, Han Xinzhi, Márfai Dóra, Masa Barnabás, Medgyesi Júlia, Somogyi Dóra, Wodala Gréta Klára. 3 points: 4 students. 2 points: 2 students. 1 point: 2 students. Unfair, not evaluated: 3 solutionss.
Problems in Mathematics of KöMaL, February 2024
