 Problem C. 1804. (March 2024)
Problem C. 1804. (March 2024)
C. 1804. In triangle \(\displaystyle ABC\) let \(\displaystyle D\), \(\displaystyle E\) and \(\displaystyle F\) denote the midpoints of the sides \(\displaystyle BC\), \(\displaystyle CA\) and \(\displaystyle AB\), respectively. Let \(\displaystyle K_a\), \(\displaystyle K_b\) and \(\displaystyle K_c\) denote the centers of the incircles of triangles \(\displaystyle AFE\), \(\displaystyle BDF\) and \(\displaystyle CED\), respectively. Prove that the sum of the areas of quadrilaterals \(\displaystyle K_aFDE\), \(\displaystyle K_bDEF\) and \(\displaystyle K_cEFD\) equals the area of triangle \(\displaystyle ABC\).
Proposed by Bálint Bíró, Eger
(5 pont)
Deadline expired on April 10, 2024.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás.
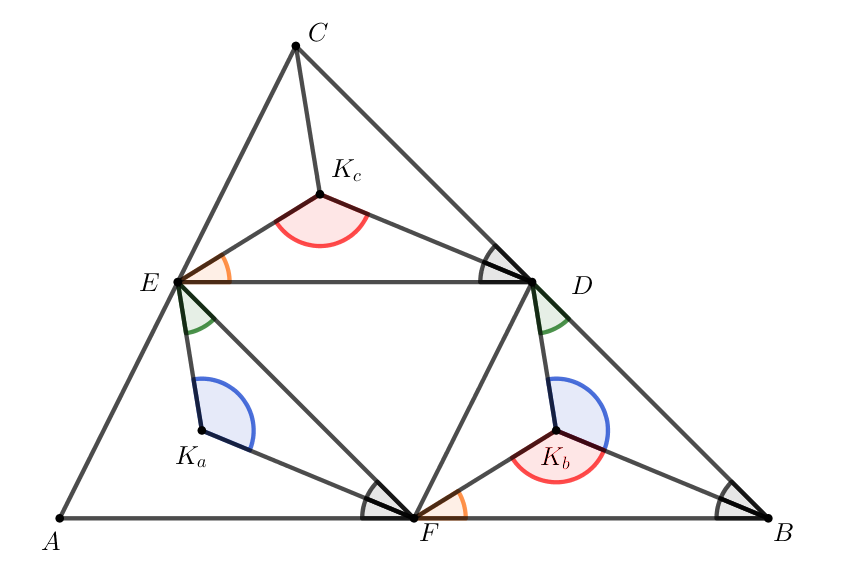
Az \(\displaystyle ABC\) háromszög középvonalai az \(\displaystyle EF\), \(\displaystyle FD\) és \(\displaystyle DE\) szakaszok. Ebből következik, hogy \(\displaystyle EF\parallel CB\), \(\displaystyle FD\parallel AC\), \(\displaystyle DE\parallel BA\), és \(\displaystyle \displaystyle{EF=\frac{1}{2}CB}\), \(\displaystyle \displaystyle{FD=\frac{1}{2}AC}\), \(\displaystyle \displaystyle{DE=\frac{1}{2}BA}\). A megfelelő szögek páronkénti egyenlőségéből és a megfelelő szakaszok hosszából következik, hogy \(\displaystyle ABC \triangle \sim AFE \triangle\), valamint \(\displaystyle AFE\triangle \cong FBD \triangle \cong EDC \triangle \cong DEF \triangle\), továbbá az is igaz, hogy
| \(\displaystyle (1)\) | \(\displaystyle \frac{T_{DEF}}{T_{ABC}}=\Bigg(\frac{1}{2}\Bigg)^2=\frac{1}{4}.\) |
A feladatban szereplő területösszeget jelöljük \(\displaystyle S\)-sel:
\(\displaystyle S=T_{K_aFDE}+T_{K_bDEF}+T_{K_cEFD}.\)
Mindhárom négyszöget két-két háromszögre vághatunk, így a területösszegekre igaz, hogy:
| \(\displaystyle (2)\) | \(\displaystyle T_{K_aFDE}=T_{DEF}+T_{EK_aF}, \) |
| \(\displaystyle (3)\) | \(\displaystyle T_{K_bDEF}=T_{DEF}+T_{DFK_b}, \) |
| \(\displaystyle (4)\) | \(\displaystyle T_{K_cEFD}=T_{DEF}+T_{K_cED}. \) |
Ha ezeket összeadjuk, azt kapjuk, hogy \(\displaystyle (2)+(3)+(4)\):
| \(\displaystyle (5)\) | \(\displaystyle S=3\cdot T_{DEF} + T_{EK_aF} + T_{DFK_b} + T_{K_cED}. \) |
Tudjuk, hogy az \(\displaystyle AFE\triangle \cong FBD \triangle\), és a beírt kör középpontja a belső szögfelezők metszéspontja, ezért \(\displaystyle EK_a \parallel DK_b\), \(\displaystyle K_aF \parallel K_bB\), továbbá \(\displaystyle EF \parallel DB\) és \(\displaystyle EF=DB\), ezért az alábbi egybevágóság teljesül:
\(\displaystyle EK_aF \triangle \cong DK_bB\triangle, \)
és ugyanígy igaz, hogy
\(\displaystyle K_cED \triangle \cong K_bFB \triangle,\hspace{0.3cm}\text{tehát} \)
\(\displaystyle T_{EK_aF} + T_{DFK_b} + T_{K_cED} = T_{DK_bB} + T_{DFK_b} + T_{K_bFB} = T_{FBD}=T_{DEF}. \)
Ebből, az (5)-ből és az (1)-ből következik, hogy
\(\displaystyle S=4\cdot T_{DEF}=T_{ABC}.\)
Statistics:
154 students sent a solution. 5 points: 84 students. 4 points: 26 students. 3 points: 10 students. 2 points: 3 students. 1 point: 4 students. Unfair, not evaluated: 9 solutionss. Not shown because of missing birth date or parental permission: 10 solutions.
Problems in Mathematics of KöMaL, March 2024
