 Problem C. 1807. (March 2024)
Problem C. 1807. (March 2024)
C. 1807. In triangle \(\displaystyle ABC\) angles satisfy \(\displaystyle 2\beta = 3\gamma\). Let points \(\displaystyle D\) and \(\displaystyle E\) be chosen on side \(\displaystyle AC\) such that \(\displaystyle BD\) and \(\displaystyle BE\) trisect angle \(\displaystyle \beta\), and point \(\displaystyle D\) is located between points \(\displaystyle A\) and \(\displaystyle E\). Further, let \(\displaystyle F\) denote the intersection of side \(\displaystyle AB\) and the angle bisector of \(\displaystyle \gamma\). Prove that \(\displaystyle BE\) and \(\displaystyle DF\) are parallel.
(Swiss competition problem)
(5 pont)
Deadline expired on April 10, 2024.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Mivel \(\displaystyle 2\beta=3\gamma\), ezért \(\displaystyle \displaystyle{\frac{\beta}{3}=\frac{\gamma}{2}=\varphi}\). Használjuk ezt a jelölést az alábbi ábrán!
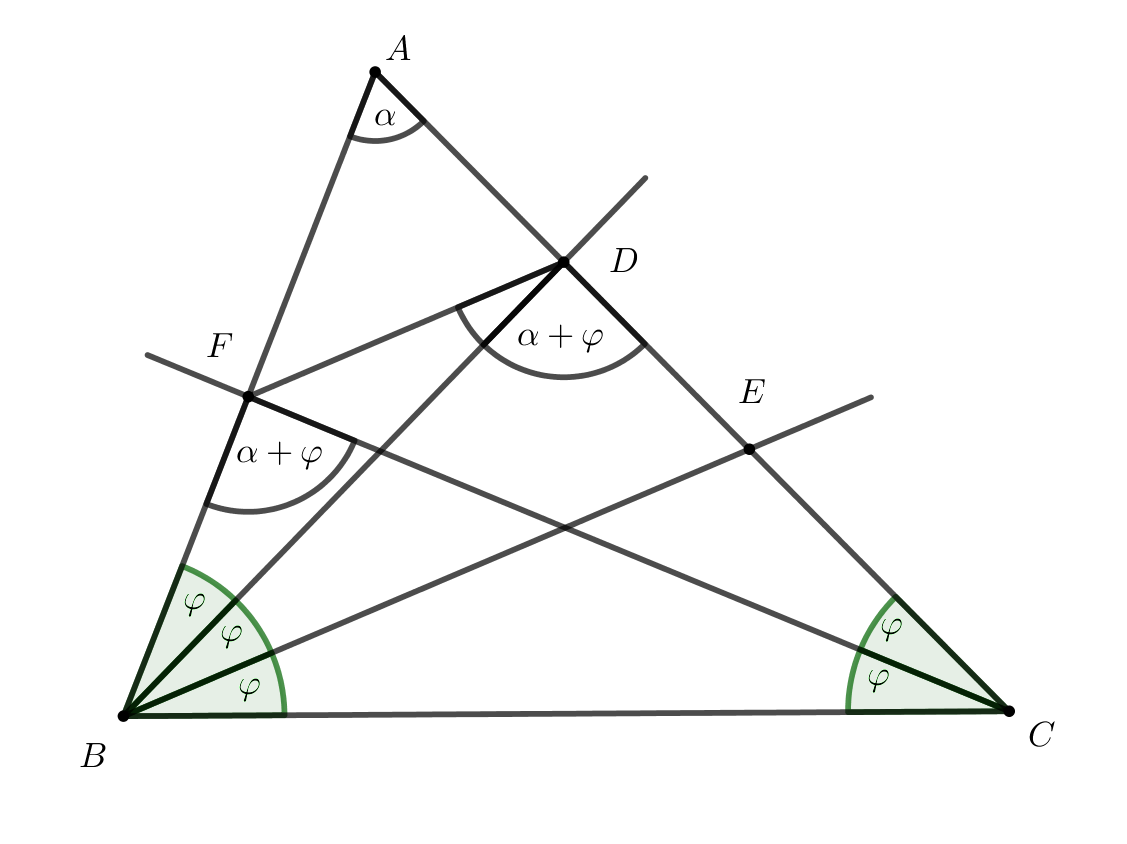
Bármely háromszög belső szögeinek összege \(\displaystyle 180^{\circ}\). Írjuk fel ezt az \(\displaystyle ABC\triangle\)-re:
| \(\displaystyle (1)\) | \(\displaystyle \alpha+5\varphi=180^{\circ}. \) |
Ezt az összefüggést alkalmazva a \(\displaystyle BCD \triangle\)-re és a \(\displaystyle BCF\triangle\)-re, azt kapjuk, hogy
\(\displaystyle BDC\sphericalangle=\alpha+\varphi, \hspace{0.2 cm} \text{és}\)
\(\displaystyle BFC\sphericalangle =\alpha+\varphi.\)
Ez azt jelenti, hogy az \(\displaystyle F\) és a \(\displaystyle D\) pontok rajta vannak a \(\displaystyle BC\) szakasz fölé rajzolt \(\displaystyle \alpha+\varphi\) nagyságú egyik látószögköríven, tehát a \(\displaystyle BCDF\) húrnégyszög (*).
Ebből következően:
| \(\displaystyle (2)\) | \(\displaystyle FBC\sphericalangle+FDC\sphericalangle=180^{\circ}. \) |
Az \(\displaystyle FDC\sphericalangle\)-re írjuk fel, amit már tudunk:
| \(\displaystyle (3)\) | \(\displaystyle FDC\sphericalangle=FDB\sphericalangle+(\alpha+\varphi).\) |
A (3) és az (1) segítségével írjuk át a (2) összefüggést, és rendezzük.
\(\displaystyle 3\varphi+FDB\sphericalangle+\alpha+\varphi=180^{\circ}=\alpha+5\varphi.\)
| \(\displaystyle (4)\) | \(\displaystyle FDB\sphericalangle=\varphi. \) |
Azt kaptuk tehát, hogy \(\displaystyle EBD\sphericalangle=FDB\sphericalangle\), vagyis az \(\displaystyle EBD\sphericalangle\) és az \(\displaystyle FDB\sphericalangle\) váltószögek. Ebből következik, hogy \(\displaystyle BE\parallel DF\).
Megjegyzés. A (*) jeltől a (4) egyenlőségig akár a következőképp is eljuthatunk:
\(\displaystyle BCDF\) húrnégyszög, tehát a köré írható kör \(\displaystyle C\)-t nem tartalmazó \(\displaystyle BF\) ívéhez tartozó kerületi szögek egyenlők, tehát
\(\displaystyle BCF\sphericalangle=\varphi=FDB\sphericalangle.\)
Statistics:
37 students sent a solution. 5 points: Baksa Anna, Balogh Péter, Bencze Mátyás, Braun Zsófia, Gyuricsek Ákos, Inokai Ádám, Iván Máté Domonkos, Márfai Dóra, Monoczki Máté, Nagy 292 Korina, Szabó Donát, Volford Barnabás, Wodala Gréta Klára, Žigo Boglárka. 4 points: Gál András, Nagy Huba, Németh Hanna Júlia , Petró Péter, Simon Bálint, Somogyi Dóra, Török Eszter Júlia. 3 points: 4 students. 2 points: 1 student. 0 point: 6 students.
Problems in Mathematics of KöMaL, March 2024
