 Problem C. 1834. (December 2024)
Problem C. 1834. (December 2024)
C. 1834. Three handsome princes competed for the hand of the beautiful daughter of the Blue King: the Red Prince, the White Prince, and the Green Prince. The first trial was the test of good taste. The princes were each given a regular blue 20-sided polygon and were allowed to color any part of it with their own color, as tastefully as possible. What the princess did not tell them was that she had already decided in advance: anyone who painted more than one-fifth of the 20-sided polygon with their own color would be considered too egotistical and therefore would not be allowed to continue competing for her hand. The princes created the following patterns.
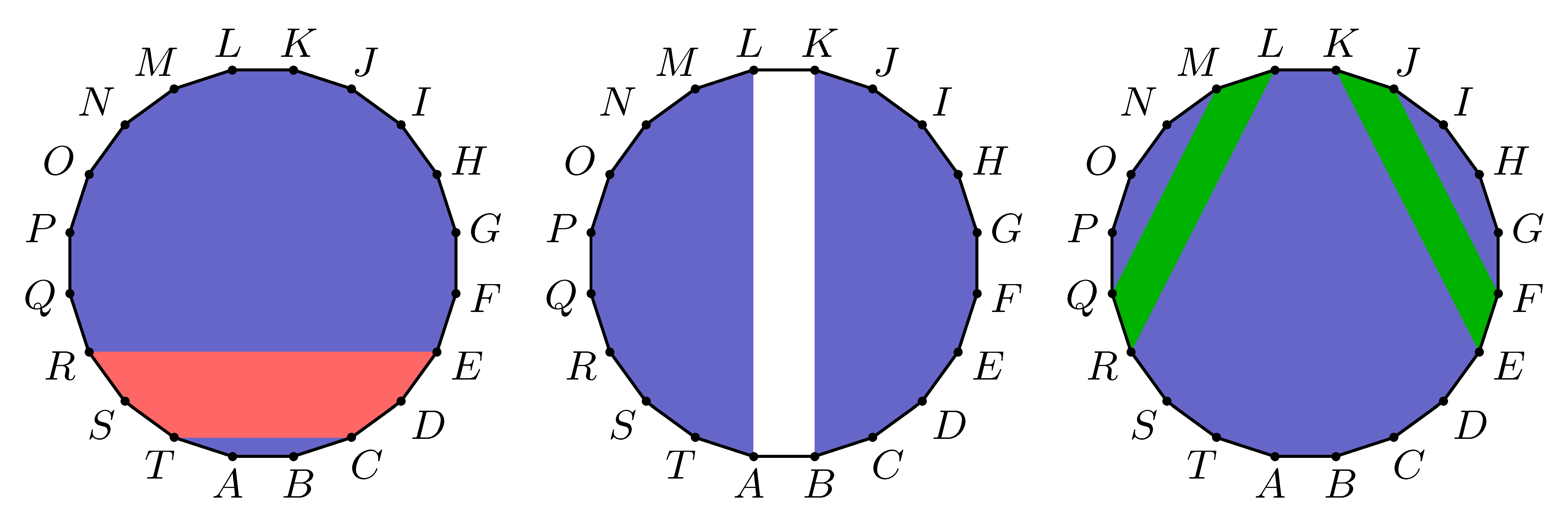
Which of them advanced to the next round of the trials? (Where the task was actually to defeat and eat a seven-headed dragon, but that's another math problem altogether.)
Proposed by: Zoltán Bertalan, Békéscsaba
(5 pont)
Deadline expired on January 10, 2025.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Használjuk a feladat ábráit, a hercegek által kijelölt síkidomok területét jelölje rendre \(\displaystyle T_{\text{piros}}\), \(\displaystyle T_{\text{fehér}}\) és \(\displaystyle T_{\text{zöld}}\), a szabályos húszszögét pedig \(\displaystyle T\), továbbá a szabályos sokszög köré írható kör középpontját \(\displaystyle X\). A húszszög egy oldalához tartozó egyenlő szárú háromszög szárai legyenek \(\displaystyle r\) hosszúságúak, az általuk bezárt szög pedig \(\displaystyle 18^{\circ}\), így egy ilyen kis háromszög területe
\(\displaystyle \displaystyle{\frac{r^2\cdot \sin{18^{\circ}}}{2}},\)
a húszszög területe pedig:
\(\displaystyle T=20\cdot \frac{r^2\cdot \sin{18^{\circ}}}{2}=10\cdot r^2\cdot \sin{18^{\circ}}.\)
A piros terület a következőképp számolható:
\(\displaystyle T_{\text{piros}}=T_{XRST}+T_{XTC}+T_{XCDE}-T_{XRE}=4\cdot \frac{r^2\cdot \sin{18^{\circ}}}{2}+\frac{r^2\cdot \sin{(3\cdot 18^{\circ})}}{2}-\frac{r^2\cdot \sin{(7\cdot 18^{\circ})}}{2}.\)
Az utolsó két tag egyenlő, hiszen \(\displaystyle (7\cdot 18^{\circ})=180^{\circ}-(3\cdot 18^{\circ})\), ezért \(\displaystyle \sin{(3\cdot 18^{\circ}})=\sin{(7\cdot 18^{\circ})}\), tehát
\(\displaystyle T_{\text{piros}}=2\cdot r^2\cdot \sin{18^{\circ}}=\frac{T}{5}.\)
A fehér területet, vagyis \(\displaystyle T_{\text{fehér}}\)-et két-két háromszögből fogjuk összerakni:
\(\displaystyle T_{\text{fehér}}=T_{ABKL}=T_{XAB}+T_{XBK}+T_{XKL}+T_{XLA}=2\cdot \frac{r^2\cdot \sin{18^{\circ}}}{2}+2\cdot \frac{r^2\cdot \sin{(9\cdot18^{\circ})}}{2}. \)
De a fenti megfontolás alapján az utolsó két tag itt is egyenlő, hiszen \(\displaystyle \sin{18^{\circ}}=\sin{(9\cdot18^{\circ})}\). Emiatt:
\(\displaystyle T_{\text{fehér}}=2\cdot r^2\cdot \sin{18^{\circ}}=\frac{T}{5}.\)
A \(\displaystyle T_{\text{zöld}}\)-et szintén két részből rakhatjuk össze:
\(\displaystyle T_{\text{zöld}}=2\cdot T_{LMQR}=2\cdot \big(T_{XLM}+T_{XMQ}+T_{XQR}-T_{XLR}\big)=2\cdot \Bigg(2\cdot \frac{r^2\cdot \sin{18^{\circ}}}{2}+\frac{r^2\cdot \sin{(4\cdot18^{\circ})}}{2}-\frac{r^2\cdot \sin{(6\cdot 18^{\circ})}}{2} \Bigg).\)
A nagy zárójelben levő tagok közül az utolsó kettő ismét egyenlő, ezért:
\(\displaystyle T_{\text{zöld}}=2\cdot r^2\cdot \sin{18^{\circ}}=\frac{T}{5}.\)
Mivel mindegyik herceg azonos területű részét színezte ki a húszszögnek, ezért mindhárman továbbjutottak, vagyis boldogan készülhetnek a próbák következő fordulójára.
Statistics:
129 students sent a solution. 5 points: 57 students. 4 points: 8 students. 3 points: 8 students. 2 points: 17 students. 1 point: 3 students. 0 point: 16 students. Not shown because of missing birth date or parental permission: 11 solutions.
Problems in Mathematics of KöMaL, December 2024
