Problem C. 1844. (February 2025)

C. 1844. Ági uses red and Laci uses blue to color the squares in an \(\displaystyle n\times n\) white board. Let \(\displaystyle (i,j)\) denote the square in the \(\displaystyle i^{\text{th}}\) row and \(\displaystyle j^{\text{th}}\) coloumn. In the first round Ági colors the squares in the main diagonal (from the top left to the bottom right) red. Now they take turns: if Laci colors square \(\displaystyle (i,j)\) blue, then Ági colors \(\displaystyle (j,i)\) red. They color every square exactly once. The \(\displaystyle k^{\text{th}}\) row is special if for every blue \(\displaystyle (k,j)\) there exists \(\displaystyle l\) such that both \(\displaystyle (k,l)\) and \(\displaystyle (l,j)\) is red. Prove that after finishing the coloring Ági is guaranteed to find a special row.

Proposed by: Zoltán Paulovics, Budapest

(5 pont)

Deadline expired on March 10, 2025.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. A szimmetrikus színezési feltétel miatt – azaz hogy \(\displaystyle (i;j)\) és \(\displaystyle (j;i)\) közül pontosan az egyik piros – legfeljebb egy csupa piros sor létezik. A csupa piros sor nyilván különleges, hiszen nincs olyan (kék) mezője, melyre teljesülnie kellene a megadott feltételnek. Feltehető tehát, hogy nincs csupa piros sor.

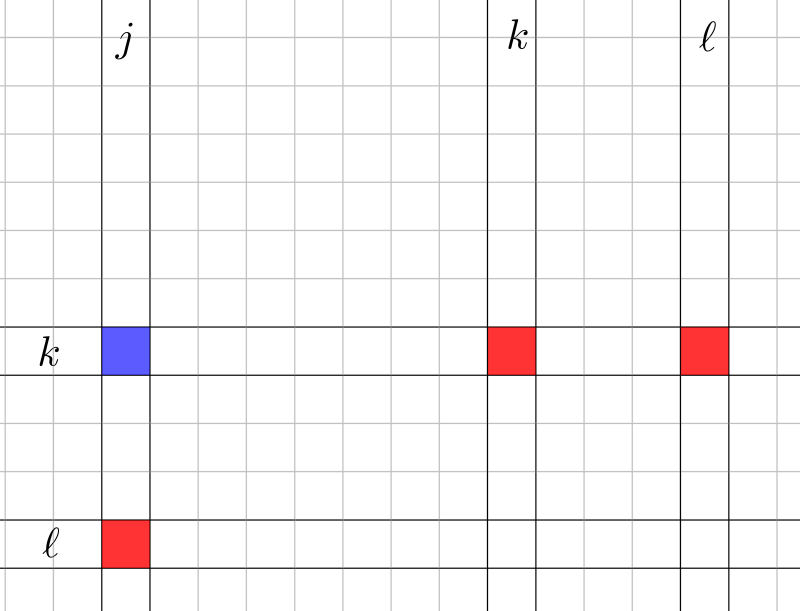
1. ábra. A különlegesség feltétele: bármely kék \(\displaystyle (k;j)\) esetén létezzen \(\displaystyle l\), hogy \(\displaystyle (k;l)\) és \(\displaystyle (l;j)\) is piros

Indirekt módon bizonyítunk: tegyük fel, hogy Ági nem talál különleges sort, azaz nincs olyan sor, amelyre bármely kék \(\displaystyle (k;j)\) mező esetén létezne \(\displaystyle l\), hogy a \(\displaystyle (k;l)\) és az \(\displaystyle (l;j)\) mezők is pirosak. Tehát bármely \(\displaystyle k\) sorra teljesül, hogy létezik olyan \(\displaystyle j\), melyre a \(\displaystyle (k;j)\) mező kék, és ha valamely \(\displaystyle l\)-re a \(\displaystyle (k;l)\) mező piros, úgy az \(\displaystyle (l;j)\) mező kék.

Ha viszont az \(\displaystyle (l;j)\) mező kék, úgy – a szimmetrikus színezési szabály miatt – a \(\displaystyle (j;l)\) mező piros. Azaz, ha a \(\displaystyle (k;l)\) mező piros, vagyis a \(\displaystyle k.\) sorban az \(\displaystyle l.\) oszlop piros, úgy a \(\displaystyle j.\) sorban is piros. Következésképpen a \(\displaystyle j.\) sorban legalább annyi piros van, mint a \(\displaystyle k.\) sorban. Sőt, több is, hiszen a \(\displaystyle (k;j)\) mező kék, míg a \(\displaystyle (j;k)\) mező piros. Az indirekt feltétel szerint nincs különleges sor, így tehát bármely sorhoz létezik olyan sor, amelyben több piros mező található, mint benne. Ez nyilvánvalóan ellentmondás.

Statistics:

71 students sent a solution.
5 points:	Bencze Mátyás, Bodó Rókus Dániel, Budai Máté, Iván Máté Domonkos, Kun Zsófia, Lovas Márk, Maróti Olga, Molnár-Sáska Tamás, Nagypál Katóca, Pázmándi Renáta .
4 points:	Pálóczi Bálint Tamás, Rózsa Zsombor.
3 points:	3 students.
1 point:	43 students.
0 point:	1 student.
Not shown because of missing birth date or parental permission:	4 solutions.

Problems in Mathematics of KöMaL, February 2025