 Problem C. 1854. (April 2025)
Problem C. 1854. (April 2025)
C. 1854. Circles \(\displaystyle k_1\) and \(\displaystyle k_2\) intersect each other in points \(\displaystyle A\) and \(\displaystyle B\) such that circle \(\displaystyle k_2\) passes through center \(\displaystyle K\) of circle \(\displaystyle k_1\). Let's choose point \(\displaystyle S\) on circle \(\displaystyle k_2\) such that \(\displaystyle S\) is closer to point \(\displaystyle A\) than to point \(\displaystyle B\), and it's not in the interior of circle \(\displaystyle k_1\). Let line \(\displaystyle BS\) intersect circle \(\displaystyle k_1\) at point \(\displaystyle D\) for the second time, and let line \(\displaystyle AD\) intersect circle \(\displaystyle k_2\) at point \(\displaystyle T\) for the second time. Prove that \(\displaystyle KT\) is perpendicular to \(\displaystyle BS\).
Greek competition problem
(5 pont)
Deadline expired on May 12, 2025.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Tekintsük a feltételeknek megfelelően készített alábbi ábrát, amelyen a
\(\displaystyle DAK\sphericalangle=\alpha;\quad KBD\sphericalangle=\beta;\quad TDB\sphericalangle=\delta;\quad KTD\sphericalangle=\tau\)
szögeket jelöltük meg.
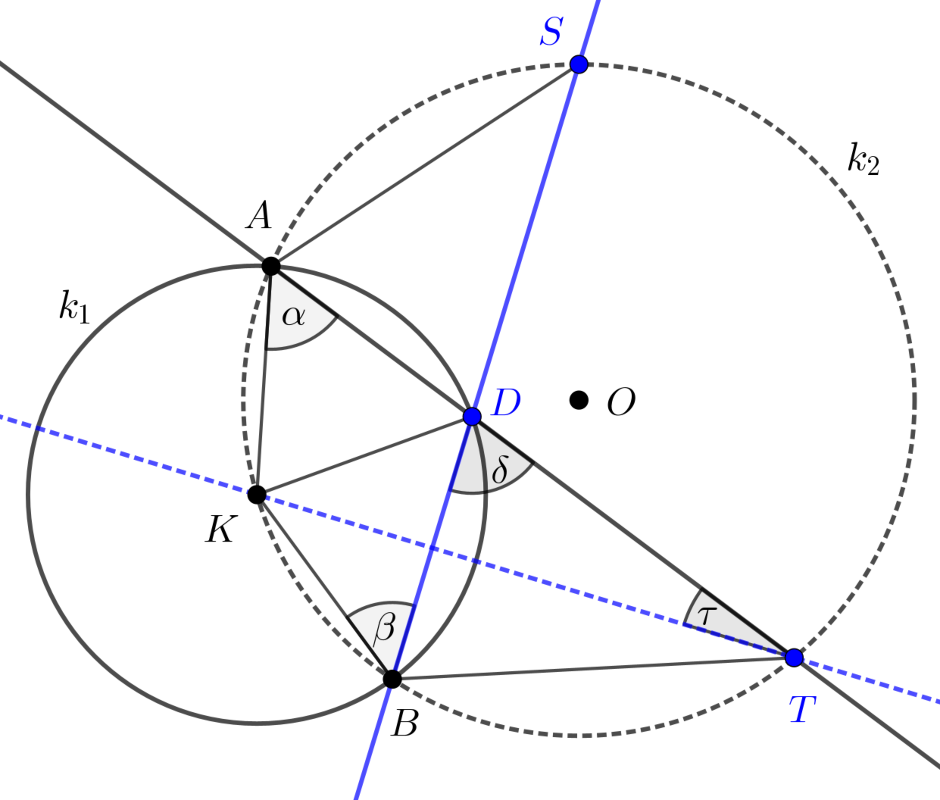
Mivel \(\displaystyle KA\), \(\displaystyle KB\) és \(\displaystyle KD\) a \(\displaystyle k_1\) kör sugarai, ezért a \(\displaystyle DAK\) és \(\displaystyle BDK\) egyenlő szárú háromszögek és így
| \(\displaystyle (1)\) | \(\displaystyle KDA\sphericalangle=\alpha;\quad BDK\sphericalangle=\beta.\) |
A \(\displaystyle TDA\sphericalangle\) egyenesszög, tehát a közös \(\displaystyle D\) csúcsú három szög összege \(\displaystyle 180^{\circ}\), azaz (1) felhasználásával
| \(\displaystyle (2)\) | \(\displaystyle \alpha+\beta+\delta=180^{\circ}.\) |
Elegendő megmutatnunk, hogy \(\displaystyle \delta+\tau=90^{\circ}\), mert ha ez igaz, akkor \(\displaystyle KT\) merőleges \(\displaystyle BS\)-re.
A \(\displaystyle k_2\) körben a \(\displaystyle KA\) és \(\displaystyle KB\) húrok hossza egyenlő, emiatt a hozzájuk tartozó ívek hossza is egyenlő, tehát a kerületi szögek tétele alapján \(\displaystyle KTD\sphericalangle=BTK\sphericalangle=\tau\), ezért \(\displaystyle BTA\sphericalangle=2\tau\). Ez azt jelenti, hogy a \(\displaystyle k_2\) körnek a \(\displaystyle K\) pontot is tartalmazó ívéhez \(\displaystyle 2\tau\) nagyságú kerületi szög tartozik, ebből ugyancsak a kerületi szögek tétele segítségével adódik, hogy
| \(\displaystyle (3)\) | \(\displaystyle BSA\sphericalangle=DSA\sphericalangle=2\tau.\) |
Az \(\displaystyle ADS\) háromszögben a csúcsszögek egyenlősége miatt \(\displaystyle ADS\sphericalangle=\delta\). Az \(\displaystyle AKBS\) négyszög húrnégyszög, amelyben a szemben levő szögek összege \(\displaystyle 180^{\circ}\), ezért
\(\displaystyle \alpha+\beta+SAD\sphericalangle=180^{\circ},\)
ebből (2) szerint
| \(\displaystyle (4)\) | \(\displaystyle SAD\sphericalangle=\delta\) |
következik. Az \(\displaystyle ADS\) háromszögben tehát a szögek összege \(\displaystyle 2\delta+2\tau=180^{\circ}\), vagyis
\(\displaystyle \delta+\tau=90^{\circ},\)
és éppen ezt akartuk igazolni. Tehát \(\displaystyle KT\) valóban merőleges \(\displaystyle BS\)-re.
Megjegyzés. Egyszerűen bizonyítható, hogy a feladat állítása nem csak a feladatban megfogalmazott feltételek mellett teljesül, hanem minden \(\displaystyle k_2\) körön levő \(\displaystyle S\) pont esetén. Különleges eset az, amikor \(\displaystyle S\) azonos \(\displaystyle B\)-vel, ekkor ha a \(\displaystyle BS\) egyenesnek a \(\displaystyle k_2\) kör a \(\displaystyle B\)-beli érintőjét tekintjük, akkor a feladat állítása érvényben marad. Hasonlóan különleges eset az, amikor \(\displaystyle A=S\), ekkor \(\displaystyle A=S=D\) és az \(\displaystyle AD\) egyenes a \(\displaystyle k_1\) kör \(\displaystyle A\) pontbeli érintője lesz, és a feladat állítása így is megmarad, ahogy akkor is, ha \(\displaystyle S=K\). Végül, ha az \(\displaystyle S\) pont és a \(\displaystyle K\)-nak az \(\displaystyle O\)-val átellenes pontja esik egybe, akkor \(\displaystyle BS\) a \(\displaystyle k_1\) kör \(\displaystyle B\)-beli érintője, továbbá \(\displaystyle B=D=T\) és világos, hogy \(\displaystyle KT\) ekkor is merőleges \(\displaystyle BS\)-re.
Statistics:
87 students sent a solution. 5 points: 51 students. 4 points: 8 students. 3 points: 5 students. 2 points: 1 student. 1 point: 2 students. 0 point: 1 student. Not shown because of missing birth date or parental permission: 11 solutions.
Problems in Mathematics of KöMaL, April 2025
