 Problem C. 1871. (October 2025)
Problem C. 1871. (October 2025)
C. 1871. The line through focus \(\displaystyle F\) of the parabola \(\displaystyle x^2-6x-4y+9=0\) and an arbitrary point \(\displaystyle P\) of the parabola intersects the parabola at point \(\displaystyle Q\) for the second time. Find the equation corresponding to the locus of the midpoints of line segment \(\displaystyle PQ\).
Proposed by Bálint Bíró, Eger
(5 pont)
Deadline expired on November 10, 2025.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. A parabola egyenletét átírhatjuk a \(\displaystyle 4y=x^2-6x+9=(x-3)^2\) alakba, ahonnan
| \(\displaystyle (1)\) | \(\displaystyle \displaystyle{y=\frac{1}{4}\big(x-3\big)^2}.\) |
(1) szerint a parabola tengelye párhuzamos az \(\displaystyle y\)-tengellyel, csúcspontja a \(\displaystyle C(3;0)\) pont, paramétere pedig \(\displaystyle p=2\). Ezekből az is következik, hogy a parabola fókuszpontja \(\displaystyle F(3; 1)\) (vezéregyenese az \(\displaystyle y=-2\) egyenes).
Az \(\displaystyle F\) ponton átmenő egyenesek egyenletét \(\displaystyle y=mx+b\) alakba írhatjuk, ezek átmennek az \(\displaystyle F\) ponton, tehát \(\displaystyle 1=3m+b\) alapján az egyenesek egyenlete
| \(\displaystyle (2)\) | \(\displaystyle y=mx+1-3m.\) |
A feltételek alapján kizárjuk az \(\displaystyle F\) ponton átmenő, az \(\displaystyle y\)-tengellyel párhuzamos egyenest.
Az \(\displaystyle F\) ponton átmenő \(\displaystyle PQ\) egyenes és a parabola közös pontjait az (1)-(2) egyenletrendszer megoldásából kaphatjuk meg. A két egyenlet jobb oldalait egyenlővé téve, a műveletek elvégzése és rendezés után az
\(\displaystyle x^2+(-6-4m)x+5+12m=0\)
másodfokú egyenletet kapjuk. Ennek az egyenletnek biztosan van két valós megoldása, mert a \(\displaystyle PQ\) egyenesnek a feltételek szerint két közös pontja kell legyen a parabolával. A megoldóképlet segítségével:
\(\displaystyle \displaystyle{x_1=3+2m+2\sqrt{m^2+1};\qquad x_2=3+2m-2\sqrt{m^2+1}},\)
ezek tehát a \(\displaystyle P\), illetve \(\displaystyle Q\) pont első koordinátái (ha az \(\displaystyle x_1\) a \(\displaystyle P\) első koordinátája, akkor \(\displaystyle x_2\) a Q ponté és megfordítva). Innen azonnal adódik a \(\displaystyle PQ\) szakasz \(\displaystyle R\) felezőpontjának első koordinátája
| \(\displaystyle (3)\) | \(\displaystyle \displaystyle{x'=\frac{x_1+x_2}{2}=3+2m}.\) |
A \(\displaystyle P\), illetve \(\displaystyle Q\) pont második koordinátáját úgy kapjuk, hogy az \(\displaystyle x_1\) és \(\displaystyle x_2\) koordinátát beírjuk a (2) egyenletbe:
\(\displaystyle \displaystyle{y_1=2m^2+2m\sqrt{m^2+1}+1;\qquad y_2=2m^2-2m\sqrt{m^2+1}+1},\)
innen az \(\displaystyle R\) felezőpont második koordinátája
| \(\displaystyle (4)\) | \(\displaystyle \displaystyle{y'=\frac{y_1+y_2}{2}=2m^2+1}.\) |
A (3) összefüggésből kifejezhetjük \(\displaystyle \displaystyle{m=\frac{x'-3}{2}}\), ezt (4)-be írva
| \(\displaystyle (5)\) | \(\displaystyle \displaystyle{y'=\frac{1}{2}\big(x'-3\big)^2+1}.\) |
Az (5) eredményből láthatóan a \(\displaystyle PQ\) szakasz \(\displaystyle R\) felezőpontjának mértani helye egy parabola, amelynek paramétere \(\displaystyle p'=1\), csúcspontja a \(\displaystyle C'(3;1)\) pont, fókuszpontja \(\displaystyle \displaystyle{F'\Big(3; \frac{3}{2}\Big)}\) (vezéregyenese a \(\displaystyle \displaystyle{y=\frac{1}{2}}\) egyenes).
Megjegyzések.
1) Az \(\displaystyle y'\) értékét úgy is megadható, hogy \(\displaystyle y_1\) és \(\displaystyle y_2\) kiszámítása, majd átlagolása helyett \(\displaystyle x'\) értékét írjuk be a (2) egyenletbe.
2) A két parabola képét megrajzolva a következő ábrát kaphatjuk.
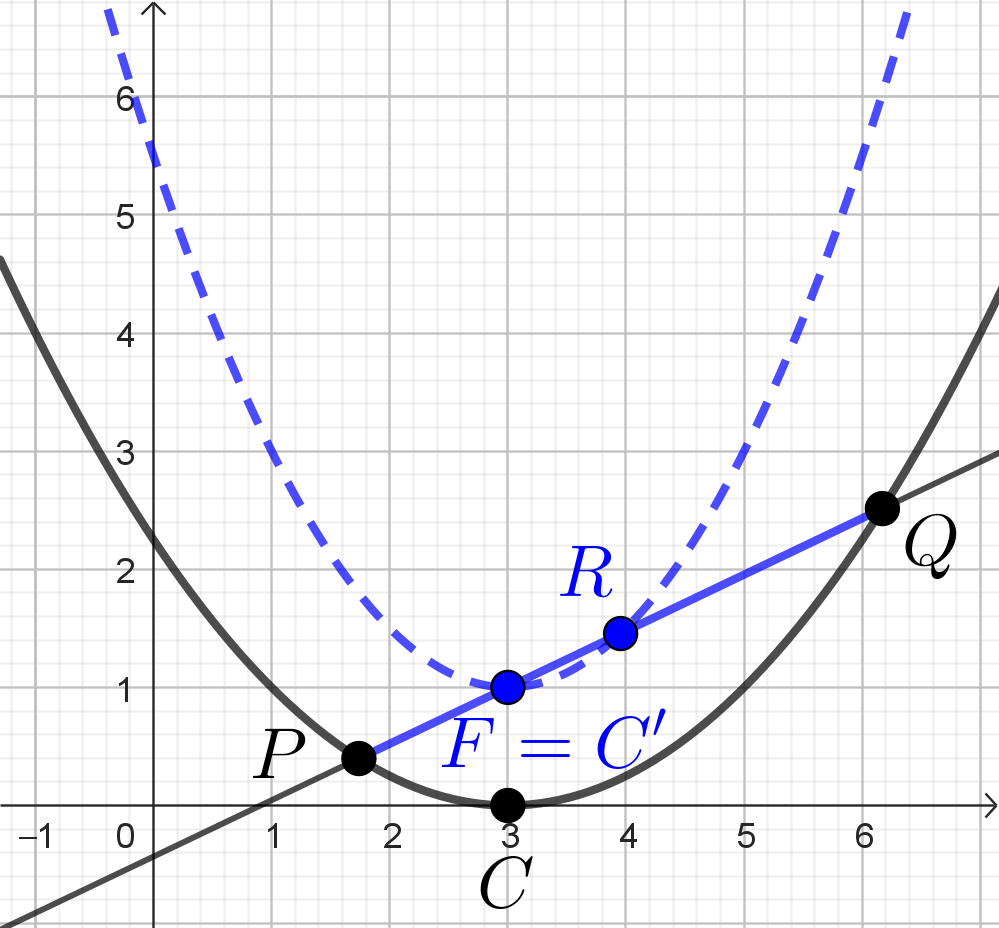
Statistics:
39 students sent a solution. 5 points: Aaishipragya Kahaly, Bán Kincső Panni, Bao Nguyen Gia, Budai Máté, Fülöp Magdaléna, Halmosi Dávid, Hetyei Dániel, Hirmann Dorottya, Kámán-Gausz Péter, Király Zsuzsanna , Németh Ábel, Papp Emese Petra, Poczai Dorottya, Válek Péter, Zádori Gellért. 4 points: Abonyi Donát Tibor, Albert Luca Liliána, Forrai Fanni, Miskolczi Máté Pál, Móricz Zsombor, Novák Zétény, Ördög Dominik, Yan Zhebeier. 3 points: 8 students. 2 points: 3 students. 1 point: 2 students. Unfair, not evaluated: 2 solutionss.
Problems in Mathematics of KöMaL, October 2025
