Problem C. 974. (January 2009)

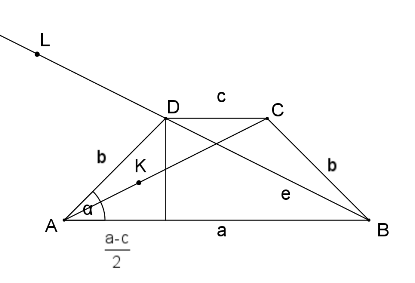
C. 974. ABCD is a cyclic trapezium. Diagonal BD is extended beyond vertex D by the length of the leg and the point L is obtained. K is the point on diagonal AC whose distance from C is equal to the leg. Prove that the areas of the rectangles formed by the line segments AB and CD and the line segments AK and BL are equal.

(5 pont)

Deadline expired on February 16, 2009.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Igazolandó: AB^.CD=AK^.BL, a szokásos jelölésekkel: ac=(e-b)(e+b). Ezt így is írhatjuk: e²=b²+ac. Az ADC háromszögben a koszinusz-tétel: e²=b²+c²-2bccos (180^o- $\alpha$ ). Elegendő lenne bizonyítani, hogy c²-2bccos (180^o- $\alpha$ )=ac, azaz: c-2bcos (180^o- $\alpha$ )=a, vagyis $\cos(180^{\circ}-\alpha)=\frac{\frac{c-a}{2}}{b}$ , illetve $\cos\alpha=\frac{\frac{a-c}{2}}{b}$ . Ez pedig igaz.

Statistics:

178 students sent a solution.

5 points: 163 students.

4 points: 4 students.

3 points: 4 students.

2 points: 2 students.

1 point: 1 student.

0 point: 1 student.

Unfair, not evaluated: 3 solutionss.

Problems in Mathematics of KöMaL, January 2009

178 students sent a solution.
5 points:	163 students.
4 points:	4 students.
3 points:	4 students.
2 points:	2 students.
1 point:	1 student.
0 point:	1 student.
Unfair, not evaluated:	3 solutionss.

Already signed up?
New to KöMaL?