 Problem C. 975. (February 2009)
Problem C. 975. (February 2009)
C. 975. In triangle ABC, the altitude drawn from vertex C intersects side AB at T. Right-angled triangles CAD and CBE are drawn on sides AC and BC on the outside, such that the right angles are at A and B. Given that AD=TB and BE=TA, prove that  CDE=
CDE= CED.
CED.
(5 pont)
Deadline expired on March 16, 2009.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás.
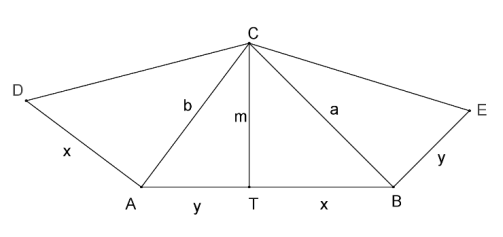
Írjuk fel a Pitagorasz-tételt az ATC és a CAD háromszögre:
| (1) | b2=y2+m2, |
| (2) | CD2=x2+b2. |
Írjuk be (2)-be az (1)-ben b2-re kapott értéket:
| (3) | CD2=x2+y2+m2. |
Írjuk fel a Pitagorasz-tételt a BTC és a CBE háromszögre:
| (4) | a2=x2+m2, |
| (5) | CE2=y2+a2. |
Írjuk be (5)-be a (4)-ben a2-re kapott értéket:
| (6) | CE2=y2+x2+m2. |
Mivel (3) és (6) jobb oldala megegyezik, ezért bal oldaluk is egyenlő: CD2=CE2. Mivel szakaszok hossza pozitív, ezért ebből CD=CE következik, tehát a egyenlő szárú. Így pedig alapon fekvő szögei egyenlők: CDE
 =CED
=CED , amit bizonyítani kellett.
, amit bizonyítani kellett.
(Ha D, C és E egy egyenesre esnek, akkor a háromszög elfajuló, és CDE =CED
=CED =0o.)
=0o.)
Statistics:
227 students sent a solution. 5 points: 213 students. 1 point: 1 student. 0 point: 6 students. Unfair, not evaluated: 7 solutionss.
Problems in Mathematics of KöMaL, February 2009
