Problem C. 987. (April 2009)

C. 987. The lengths of the sides of a triangle cut out of paper are 8 cm, 10 cm and 12 cm. The triangle is folded along a line through the common vertex so that the shortest side overlaps with the longest side. A double-layer part and a single-layer part are obtained. Prove that the single-layer part is an isosceles triangle.

(5 pont)

Deadline expired on May 15, 2009.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Készítsünk vázlatrajzot!

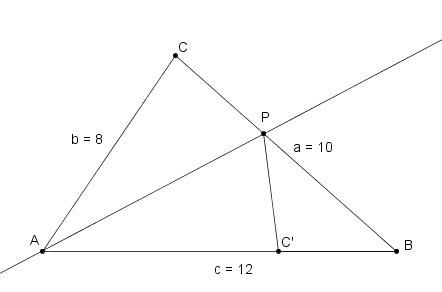
A hajtogatás következtében $APC\triangle\cong APC'\triangle$ . Ekkor CAP $\angle$ =C'AP $\angle$ , tehát a P pont az A csúcsból induló szögfelező és az a oldal metszéspontja.

Az egybevágóság miatt AC'=AC=8, így BC'=4.

A háromszög szögfelezőjének osztásarányáról szóló tétel szerint: $\frac{BP}{PC}=\frac{12}{8}$ . Legyen BP=12x és PC=8x. Ekkor 12x+8x=10, amiből $x=\frac12$ . Így $PC=8\cdot\frac12=4$ , amivel egyenlő a PC' is.

Ezzel beláttuk, hogy PC'=BC'=4, azaz a C'PB háromszög (az egyrétegű rész) valóban egyenlő szárú.

Statistics:

185 students sent a solution.

5 points: 110 students.

4 points: 49 students.

3 points: 10 students.

2 points: 2 students.

1 point: 3 students.

0 point: 3 students.

Unfair, not evaluated: 8 solutionss.

Problems in Mathematics of KöMaL, April 2009

185 students sent a solution.
5 points:	110 students.
4 points:	49 students.
3 points:	10 students.
2 points:	2 students.
1 point:	3 students.
0 point:	3 students.
Unfair, not evaluated:	8 solutionss.

Already signed up?
New to KöMaL?