 |
A G. 648. feladat (2018. október) |
G. 648. Egy kis bogár indul el egy 10 cm oldalélű fakocka \(\displaystyle P\) csúcsából. Legalább mennyi időre van szüksége a bogárnak ahhoz, hogy elérjen a kocka legtávolabbi \(\displaystyle Q\) csúcsához, ha a bogár sebessége 1 cm/s? Hányféle úton mozoghat a bogár, hogy a legrövidebb idő alatt odaérjen?
(4 pont)
A beküldési határidő 2018. november 12-én LEJÁRT.
Megoldás. A bogár két egymással érintkező oldallapon haladva juthat el \(\displaystyle P\)-ből \(\displaystyle Q\)-ba. Ezt a két lapot síkba kiterítve egy \(\displaystyle 20~\rm cm \times 10~\rm cm\) méretű téglalapot kapunk, amelynek átlója (nyilván ez felel meg a legrövidebb útnak) \(\displaystyle \sqrt{500}\approx 22{,}4\) cm hosszú. A bogár tehát leghamarabb 22,4 s alatt érhet el a \(\displaystyle P\) csúcspontból a \(\displaystyle Q\) csúcspontba.
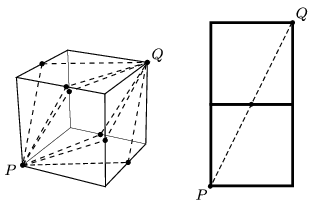
A bogár az ábrán látható hatféle útvonal bármelyikét választva ugyanannyi idő alatt ér a \(\displaystyle P\) pontból a \(\displaystyle Q\) pontba.
Statisztika:
A KöMaL 2018. októberi fizika feladatai

