Problem G. 658. (January 2019)

G. 658. Six forces are exerted on the same body at the same time: \(\displaystyle F_1=1\) N, \(\displaystyle F_2=2\) N, \(\displaystyle F_3=3\) N, \(\displaystyle F_4= 4\) N, \(\displaystyle F_5=5\) N and \(\displaystyle F_6=6\) N. The forces are all in the same plane and the angles between two adjacent forces are \(\displaystyle 60^\circ\) (i.e. the consecutive rotations of the forces are always \(\displaystyle 60^\circ\) in the same direction).

\(\displaystyle a)\) What is the vector sum of the six forces?

\(\displaystyle b)\) How should the magnitude or maybe as well the direction of force \(\displaystyle F_{2}\) be changed in order for the object to be in equilibrium?

(3 pont)

Deadline expired on February 11, 2019.

Sorry, the solution is available only in Hungarian. Google translation

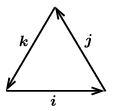
Megoldás. Tekintsük egy egységnyi oldalélű szabályos háromszög oldalait vektoroknak, és jelöljük ezeket a vektorokat \(\displaystyle \boldsymbol i\)-vel, \(\displaystyle \boldsymbol j\)-vel és \(\displaystyle \boldsymbol k\)-val, ahogy azt az 1. ábra mutatja. Nyilván fennáll, hogy \(\displaystyle \boldsymbol i+\boldsymbol j+\boldsymbol k=\boldsymbol 0\), vagyis

\(\displaystyle \boldsymbol k=-(\boldsymbol i+\boldsymbol j).\)

1. ábra

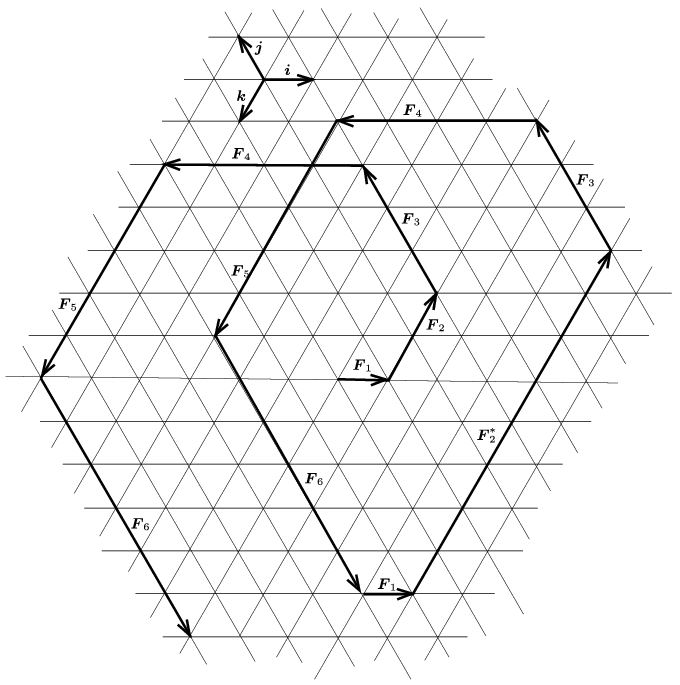
A feladat szövegének megfelelő vektorok pl. így választhatók (azok nagyságát newton egységekben mérve):

\(\displaystyle {\boldsymbol F}_1={\boldsymbol i},\qquad {\boldsymbol F}_2=-2{\boldsymbol k},\qquad {\boldsymbol F}_3=3{\boldsymbol j},\qquad {\boldsymbol F}_4=-4{\boldsymbol i},\qquad {\boldsymbol F}_5=5{\boldsymbol k},\qquad {\boldsymbol F}_6=-6{\boldsymbol j}.\)

Az eredő erő, vagyis a hat erő vektori összege:

\(\displaystyle {\boldsymbol F}_1+{\boldsymbol F}_2+{\boldsymbol F}_3+{\boldsymbol F}_4+{\boldsymbol F}_5+{\boldsymbol F}_6=-3(\boldsymbol i+\boldsymbol j)+ 3{\boldsymbol k}=6{\boldsymbol k}=-3{\boldsymbol F}_2.\)

\(\displaystyle b)\) Ha az \(\displaystyle {\boldsymbol F}_2\) erő nagyságát az eredeti érték 4-szeresére, vagyis \(\displaystyle {\boldsymbol F}^*_2=8\) N-ra növeljük, de az irányát nem változtatjuk meg, akkor az eredő erő nullává válik, a test egyensúlyba kerül.

2. ábra

Statistics:

75 students sent a solution.
3 points:	51 students.
2 points:	9 students.
1 point:	7 students.
0 point:	7 students.
Not shown because of missing birth date or parental permission:	1 solutions.

Problems in Physics of KöMaL, January 2019