Problem G. 695. (January 2020)

G. 695. Toy penguins were suspended to an unsteady room decoration. The very light rods (see the figure) were suspended at their quadrisection points such that the structure is in equilibrium. What are the masses of the second, the third, and the fourth toy penguins, if the first one has a mass of 480 g?

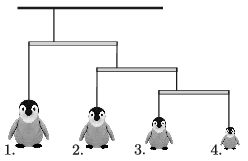
(3 pont)

Deadline expired on February 10, 2020.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Egyensúlyban mindegyik rudacska bal szélét háromszor nagyobb erő húzza, mint a jobb szélét. Ezek szerint ha a 4. pingvin súlya \(\displaystyle G_4\), akkor \(\displaystyle G_3=3\,G_4\). A középső rudacska jobb szélét \(\displaystyle G_3+G_4=4\,G_4\), a bal szélét ennek háromszorosa, vagyis \(\displaystyle G_2=12\,G_4\) erő húzza lefelé. Végül a legfelső rudacskára ható erő a bal szélénél \(\displaystyle G_1=3\cdot 16\,G_4=48\,G_4.\) A feladat szövege szerint \(\displaystyle 48\,G_4\) megegyezik 48 dkg-nyi tömeg súlyával, így a többi tömeg: \(\displaystyle m_2=12~\rm dkg\), \(\displaystyle m_3=3~\rm dkg\) és \(\displaystyle m_4=1~\rm dkg\).

Statistics:

81 students sent a solution.
3 points:	62 students.
2 points:	11 students.
1 point:	6 students.
0 point:	2 students.

Problems in Physics of KöMaL, January 2020