 |
A G. 696. feladat (2020. január) |
G. 696. Sanyi egy forrasztópákát kapott karácsonyra, és rögtön kipróbálta. Egy \(\displaystyle 2000~\Omega\)-os ellenállással párhuzamosan összeforrasztott egy \(\displaystyle 500~\Omega\)-os ellenállást, majd az egésszel sorba egy másik \(\displaystyle 500~\Omega\)-osat, végül az így kapott elrendezéssel párhuzamosan egy \(\displaystyle 600~\Omega\)-os ellenállást. Az egészet egy telepre kapcsolta, és megállapította, hogy így a \(\displaystyle 2000~\Omega\)-os ellenálláson 2 V feszültség mérhető.
\(\displaystyle a)\) Készítsük el az áramkör kapcsolási rajzát!
\(\displaystyle b)\) Mekkora a telep feszültsége?
\(\displaystyle c)\) Mekkora a telepen átfolyó áram erőssége?
(3 pont)
A beküldési határidő 2020. február 10-én LEJÁRT.
Megoldás. \(\displaystyle a)\)
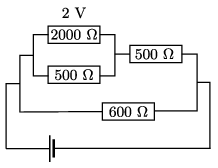
\(\displaystyle b)\) Az Ohm-törvény szerint a 2000 ohmos ellenálláson 1 mA áram folyik, a vele párhuzamos 500 ohmoson pedig 4 mA. A másik 500 ohmos ellenálláson összesen 5 mA áram folyik át, rajta eső feszöltség tehát 2,5 V. A telep feszültsége \(\displaystyle 2~{\rm V}+2{,}5~{\rm V}=4{,}5~{\rm V},\) és a 600 ohmos ellenálláson 7,5 mA folyik át.
\(\displaystyle c)\) A telepen átfolyó áram: 12,5 mA.
Statisztika:
55 dolgozat érkezett. 3 pontot kapott: Árvai Tímea, Bacsó Dániel, Bana Marcell, Bartók Vince, Beke Bálint, Bognár 171 András Károly, Cynolter Dorottya, Dobre Zsombor, Dózsa Levente, Egyházi Hanna, Fehér Anna, Fürész Tibor, Gábriel Tamás, Györe István, Helyes András, Jeszenői Sára, Juhász Júlia, Kaltenecker Balázs Bence, Klepáček László, Koczkás Árpád, Koleszár Benedek, Kovács Alex, Kovács Kinga, Köpenczei Csanád, Kuremszki Bálint, Láng Erik, Lőrinczi Gergő, Malatinszki Hanna, Medveczki Gábor József, Merza Roland, Molnár Kristóf, Móricz Benjámin, Nemeskéri Dániel, Papp Marcell Miklós, Pleva Levente, Richlik Bence, Sárvári Borka Luca, Schmercz Blanka, Stein Felix, Szabó Réka, Szécsi Ákos, Szőllősi Gergely, Tatai Ottó, Vanya Zsuzsanna, Veszprémi Rebeka Barbara. 2 pontot kapott: Buzási-Temesi Imre, Polák Mátyás , Szirmai Dénes. 1 pontot kapott: 6 versenyző. 0 pontot kapott: 1 versenyző.
A KöMaL 2020. januári fizika feladatai

