A G. 723. feladat (2020. november)

G. 723. Van egy \(\displaystyle 5\) dioptriás gyűjtőlencsénk és egy \(\displaystyle -8\) dioptriás szórólencsénk. A sötét szobába a lyukas függönyön át párhuzamos, vízszintes fénynyaláb érkezik, és kerek foltot vetít a falra. Melyik lencsét és hova kell helyeznünk, hogy a falon a folt ponttá zsugorodjon össze?

Ha most a másik lencsét is a fény útjába állítjuk, hová tegyük, hogy ismét párhuzamos fénynyalábot nyerjük, és ismét kerek fényfoltot lássunk a falon? Ez a fényfolt kisebb vagy nagyobb lesz az eredetinél?

(3 pont)

A beküldési határidő 2020. december 15-én LEJÁRT.

Megoldás. Egy lencse fókuszttávolsága (méterben mérve) a lencse dioptriájának reciproka. Eszerint a feladatban szerepló gyüjtőlencse fókusztávolsága

\(\displaystyle f_1=\frac{1}{5}\,\text{méter}=20~\rm cm,\)

a szórólencsére pedig

\(\displaystyle f_2=-\frac{1}{8}\,\text{méter}=-12{,}5~\rm cm.\)

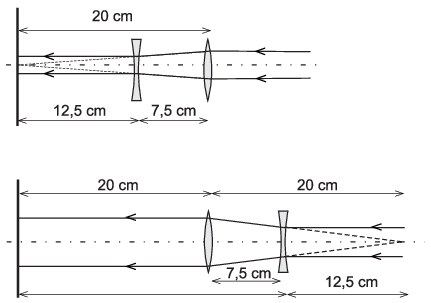
Egyetlen lencse csak akkor fókuszálhatja a párhuzamos fénynyalábot, ha az a gyüjtőlencse, és \(\displaystyle f_1=20~\)cm távol van a faltól. Egy ilyen helyzetű lencse elé vagy mögé \(\displaystyle f_2=7{,}5\) cm távolságban elhelyezett szórólencse olyan optikai eszközt alkot, amelyet a párhuzamosan érkező fénynyaláb ismét párhuzamos nyalábként hagy el, ahogy azt az ábra mutatja). (Ez az összeállítás a Galilei-féle távcső elrendezésének felel meg.)

Ezek szerint a szórólencsét a faltól vagy 20-7,5=12,5 cm, vagy 20+7,5=27,5 cm távolságbam kell elhelyeznünk. Az első esetben a falon megjelenő fényfolt 5/8-szor kisebb, a második esetben pedig 8/5-ször nagyobb, mint amekkora a lencsék nélkül látható fényfolt volt.

Statisztika:

A G. 723. feladat értékelése még nem fejeződött be.

A KöMaL 2020. novemberi fizika feladatai