 |
A G. 748. feladat (2021. május) |
G. 748. Egy magas, vízzel telt mérőhengerbe szájával lefelé fordított, 20 cm hosszú kémcsövet (Cartesius-búvárt) helyezünk úgy, hogy a kémcső felső felében levegő, alsó felében pedig víz legyen. Ekkor a kémcső úszik, zárt, felső vége kissé kiemelkedik a mérőhengerben lévő vízből. A mérőhenger tetejét gumilappal zárjuk le, majd akkora erővel nyomjuk lefelé a gumilapot, hogy ennek hatására a kémcsőben lévő levegő nyomása 5 kPa-lal megnő. Ebben a pillanatban a ,,búvár'' elindul lefelé.
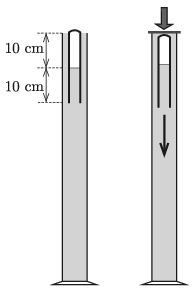
\(\displaystyle a)\) A ,,búvár'' elmerülésének a kezdetén mekkora volt a kémcsőbe zárt levegőoszlop magassága?
\(\displaystyle b)\) Legalább milyen magas a mérőhenger, ha a ,,búvár'' lent marad akkor is, amikor eltávolítjuk a gumilapot a mérőhenger tetejéről?
(4 pont)
A beküldési határidő 2021. június 15-én LEJÁRT.
Megoldás. \(\displaystyle a)\) Feltételezzük, hogy a külső légnyomás 100 kPa. 10 cm mélyen a víz hidrosztatikai nyomása közelítőleg 1 kPa. Mivel a búvár kezdetben csak ,,kicsit'' emelkedik ki a vízből, a benne lévő levegő nyomása 101 kPa.
Ha a bezárt levegő nyomását 5 kPa-lal növeljük, az 106 kPa lesz. Feltételezhetjük, hogy eközben a gáz hőmérséklete nem változik, így a Boyle–Mariotte-törvény szerint a levegőoszlop hossza
\(\displaystyle 10~{\rm cm}\cdot \frac{101}{106}=9{,}5~\rm cm\)
lesz. Ebben az állapotban a bezárt levegő és a kémcső fala által kiszorított víz súlya éppen a búvár súlyával (gyakorlatilag a kémcső súlyával) egyezik meg.
\(\displaystyle b)\) A búvár akkor marad lent a túlnyomás megszünte után is, ha a bezárt levegő hossza ott is 9,5 cm, vagyis a levegő nyomása 106 kPa, miközben a víz felszínénél a nyomás 100 kPa. A víz hidrosztatikai nyomása deciméterenként 1 kPa, tehát az edény aljára süllyedt búvárban lévő levegő alsó határa legalább 60 cm mélyen kell legyen. Ez akkor teljesül, ha a mérőhenger legalább 70,5 cm magas.
Statisztika:
25 dolgozat érkezett. 4 pontot kapott: Bencz Benedek, Buzási-Temesi Imre, Hegedűs Máté Miklós, Láng Erik, Lipóczi Levente, Molnár Kristóf, Richlik Márton, Szabó Réka, Vágó Botond, Veszprémi Rebeka Barbara, Wórum Soma. 3 pontot kapott: Cynolter Dorottya, Czirók Tamás, Jeszenői Sára, Josepovits Gábor, Kornya Gergely Csaba, Kovács Dorina , Marozsi Lenke Sára, Patricia Janecsko, Waldhauser Miklós. 2 pontot kapott: 3 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2021. májusi fizika feladatai

