Problem G. 824. (September 2023)

G. 824. A snake of length \(\displaystyle \ell\) slithered half of its length into a narrow, straight tube. The outside end of the snake can curve arbitrarily on the horizontal ground. At which points in the plane can the snake's centre of mass be located, if the snake is modelled by a flexible rope of length \(\displaystyle \ell\) with a uniform mass distribution?

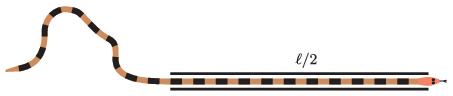
(4 pont)

Deadline expired on October 16, 2023.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Legyen a kígyó teljes tömege \(\displaystyle m\), ekkor (a tömegközéppont szempontjából) a csőben lévő része is és a kint kacskaringózó rész is egy-egy \(\displaystyle m/2\) tömegű tömegponttal helyettesíthető. Jelöljük a cső egyik végét (amelyiknél a kígyó feje van) \(\displaystyle A\)-val, a cső felezőpontját \(\displaystyle S_1\)-gyel, a cső másik végét (ahol a kígyó ,,közepe'' van) \(\displaystyle C\)-vel, a kígyó farkának helyét pedig \(\displaystyle B\)-vel (1. ábra).

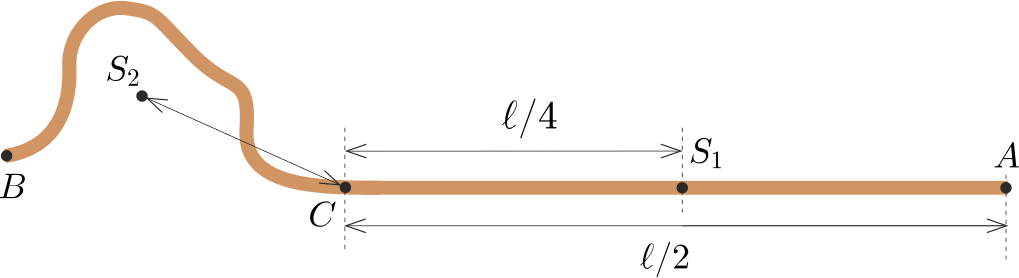
1. ábra

A kígyó első (egyenes) részének \(\displaystyle S_1\) tömegközéppontja \(\displaystyle C\)-től nyilván \(\displaystyle \ell/4\) távol van, a másik rész \(\displaystyle S_2\) tömegközéppontjának \(\displaystyle C\)-től mért távolságát pedig jelöljük \(\displaystyle r\)-rel. A kígyó alakjának ismerete nélkül \(\displaystyle r\) nagyságát nem tudjuk pontosan megadni, de azt állíthatjuk, hogy \(\displaystyle r\le \ell/4\). Ez – a továbbiakban fontos – egyenlőtlenség elég szemléletes (hiszen ha a kígyó kiegyenesedne, akkor éppen \(\displaystyle r=\ell/4\) teljesülne), de szigorú bizonyítását a Függelék tartalmazza.

Az egyenlőtlenséget felhasználva kétféle megoldás is adható a feltett kérdésre.

I. (geometriai) megoldás. A kígyó tömegközéppontja az \(\displaystyle S_1S_2\) szakasz \(\displaystyle S\) felezőpontjában található. Jelöljük \(\displaystyle CS_1\) felezőpontját (vagyis a cső nyolcadolópontját) \(\displaystyle P\)-vel (2. ábra).

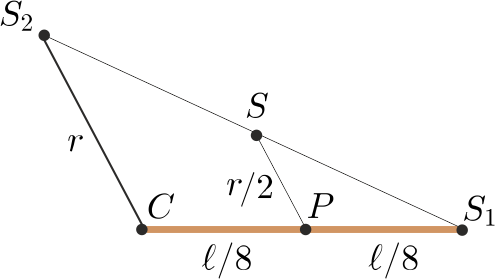
2. ábra

A \(\displaystyle CS_1S_2\) és a \(\displaystyle PS_1S\) háromszögek hasonlósága miatt

\(\displaystyle SP= \frac{r}2\le\frac{\ell}8.\)

Figyelembe véve, hogy a \(\displaystyle CS_2\) egyenes iránya tetszőleges lehet, megállapíthatjuk, hogy a kígyó \(\displaystyle S\) tömegközéppontja egy \(\displaystyle P\) középpontú, \(\displaystyle \ell/8\) sugarú körlapon található.

II. (vektoralgebrai) megoldás. Jelöljük a \(\displaystyle \overrightarrow{CS_1}\) vektort \(\displaystyle \frac14\boldsymbol{\ell}\)-lel, a \(\displaystyle \overrightarrow{CS_2}\) vektort pedig \(\displaystyle \boldsymbol r\)-rel. Ekkor \(\displaystyle C\)-ből a kígyó \(\displaystyle S\) tömegközéppontjába mutató vektor

\(\displaystyle \boldsymbol s=\frac12\left(\frac14\boldsymbol{\ell}+\boldsymbol r\right)= \frac18\boldsymbol{\ell}+\frac12\boldsymbol r.\)

Innen leolvashatjuk, hogy \(\displaystyle S\) és \(\displaystyle P\) távolosága

\(\displaystyle \left|\boldsymbol s- \frac18\boldsymbol{\ell} \right| =\frac12|\boldsymbol r|\le \frac{\ell}8.\)

A kígyó \(\displaystyle S\) tömegközéppontja tehát egy \(\displaystyle P\) középpontú, \(\displaystyle \ell/8\) sugarú körlapon (a 3. ábra sárga tartományában) helyezkedhet el.

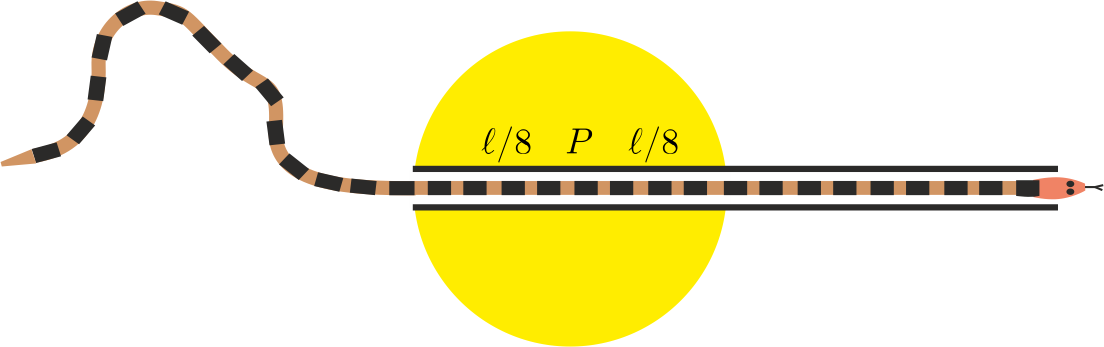
3. ábra

Függelék. Tekintsük a kígyó hátsó felét a \(\displaystyle C\) és \(\displaystyle B\) pontok között kanyargó görbe vonalnak, aminek tömegközéppontja \(\displaystyle S_2\). Ha a ,,félkígyó'' kiegyenesedne, és a \(\displaystyle CS_2\) egyenessel párhuzamos \(\displaystyle CB'\) lenne, akkor az \(\displaystyle S_2'\) tömegközéppontja \(\displaystyle C\)-tól \(\displaystyle \ell/4\) távolra kerülne.

Hasonlítsuk össze a kanyargós kígyó tetszőleges \(\displaystyle P\) pontját ugyanezen pontnak a kiegyenesedett kígyón megtalálható \(\displaystyle P'\) megfelelőjével (4. ábra). Nyilván \(\displaystyle CP\le CP'\), továbbá \(\displaystyle CP''\le CP\) (ahol \(\displaystyle P''\) a \(\displaystyle P\) pont merőleges vetülete a \(\displaystyle CB'\) egyenesen), és így

\(\displaystyle CP'\ge CP\ge CP''.\)

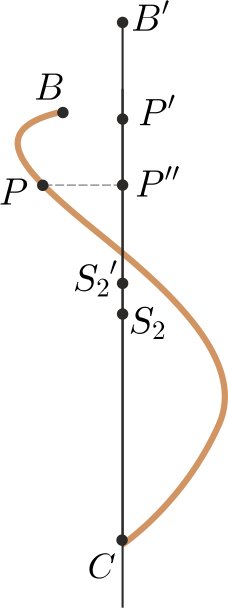
4. ábra

A görbe félkígyó tömegközéppontját a \(\displaystyle CP''\) távolságok határozzák meg. Mivel a fenti egyenlőtlenség minden \(\displaystyle P\) pontra érvényes, a tömegközéppontokra is fennáll:

\(\displaystyle r=CS_2\le CS_2'=\frac{\ell}4,\)

és éppen ezt akartuk bizonyítani.

Statistics:

42 students sent a solution.
4 points:	Blaskovics Ádám, Bohner Emese, Bús László Teodor, Csizmadia Ferenc, Derűs Ádám , Field Márton, Fülöp Magdaléna, Hajdufi Imola, Klenkó Éva Borbála, Méhes Mátyás , Porcsin Gréta, Pulka Gergely Tamás, Szabó András, Tajta Sára, Varga 511 Vivien.
3 points:	Gerlei Dániel, Schmidt Marcell, Sipos Dániel Sándor, Táborosi Sára.
2 points:	5 students.
1 point:	6 students.
0 point:	5 students.
Not shown because of missing birth date or parental permission:	6 solutions.

Problems in Physics of KöMaL, September 2023