Problem G. 862. (October 2024)

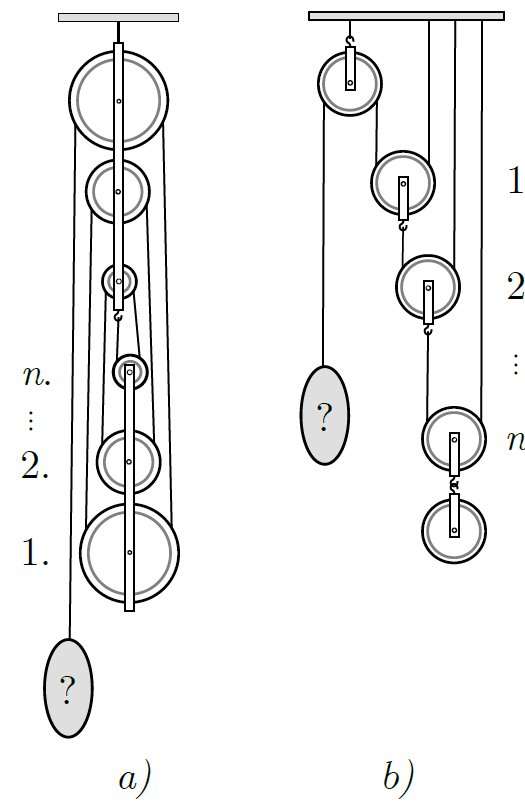
G. 862. A pulley system consists of \(\displaystyle n\) pulleys. Regardless of their size each moving pulley has the same weight of \(\displaystyle G\), and the rope can be considered ideal. How much weight should be hung on the end of the rope so that the system is in equilibrium if the pulley system

\(\displaystyle a)\) is not loaded, and arranged as shown in figure \(\displaystyle a)\);

\(\displaystyle b)\) is loaded with a pulley of weight \(\displaystyle G\) and the pulleys are arranged as shown in figure \(\displaystyle b)\)?

(4 pont)

Deadline expired on November 15, 2024.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. a) Az \(\displaystyle n\) mozgócsigát összesen \(\displaystyle 2n\) kötél tartja (mindegyik mozgócsiga jobb és bal oldalán egy-egy kötél). A kötélben végig azonos a feszítettség, tehát az \(\displaystyle n\) mozgócsiga \(\displaystyle nG\) súlyával \(\displaystyle 2nF\) erő tart egyensúlyt (\(\displaystyle 2nF=nG\)). Így a rendszer egyensúlyához \(\displaystyle F=G/2\) súlyú testet kell a kötél végére akasztani.

b) Az utolsó mozgócsiga a ráakasztott terheléssel együtt \(\displaystyle 2G\) súlyú, vagyis az utolsó mozgócsiga jobb és bal oldalához tartozó két kötélszárban a feszítőerő ennek fele, tehát \(\displaystyle G\). Az utolsó előtti mozgócsiga \(\displaystyle G\) súlyához a kötél még ugyanekkora \(\displaystyle G\) erővel járul hozzá, így az ehhez a csigához tartozó két kötélszárban szintén \(\displaystyle G\) a feszítőerő. Ugyanezt a megfontolást tehetjük rendre az összes mozgócsigára, tehát az egyes (egymástól független) kötéldarabokban mindenhol \(\displaystyle G\) a feszítőerő, vagyis az állócsigán átvetett kötél végére egy \(\displaystyle G\) súlyú testet kell akasztanunk.

Statistics:

32 students sent a solution.
4 points:	Békési Máté, Csáki Anikó, Csonka Áron, Hegedüs Márk, Horváth Zsombor, József Áron, Kovács Artúr-Lehel, Majer Veronika, Patócs 420 Péter, Sipeki Andor, Szabó András, Szighardt Anna, Szilaj Petra, Szűcs Kitti, Tóth Domonkos.
3 points:	Vízhányó Janka.
2 points:	5 students.
1 point:	6 students.
0 point:	3 students.
Unfair, not evaluated:	1 solutions.

Problems in Physics of KöMaL, October 2024