Problem G. 869. (December 2024)

G. 869. A car's front and rear wheels are at the vertices of a rectangle with sides 4 m and 2 m, as shown in the figure.

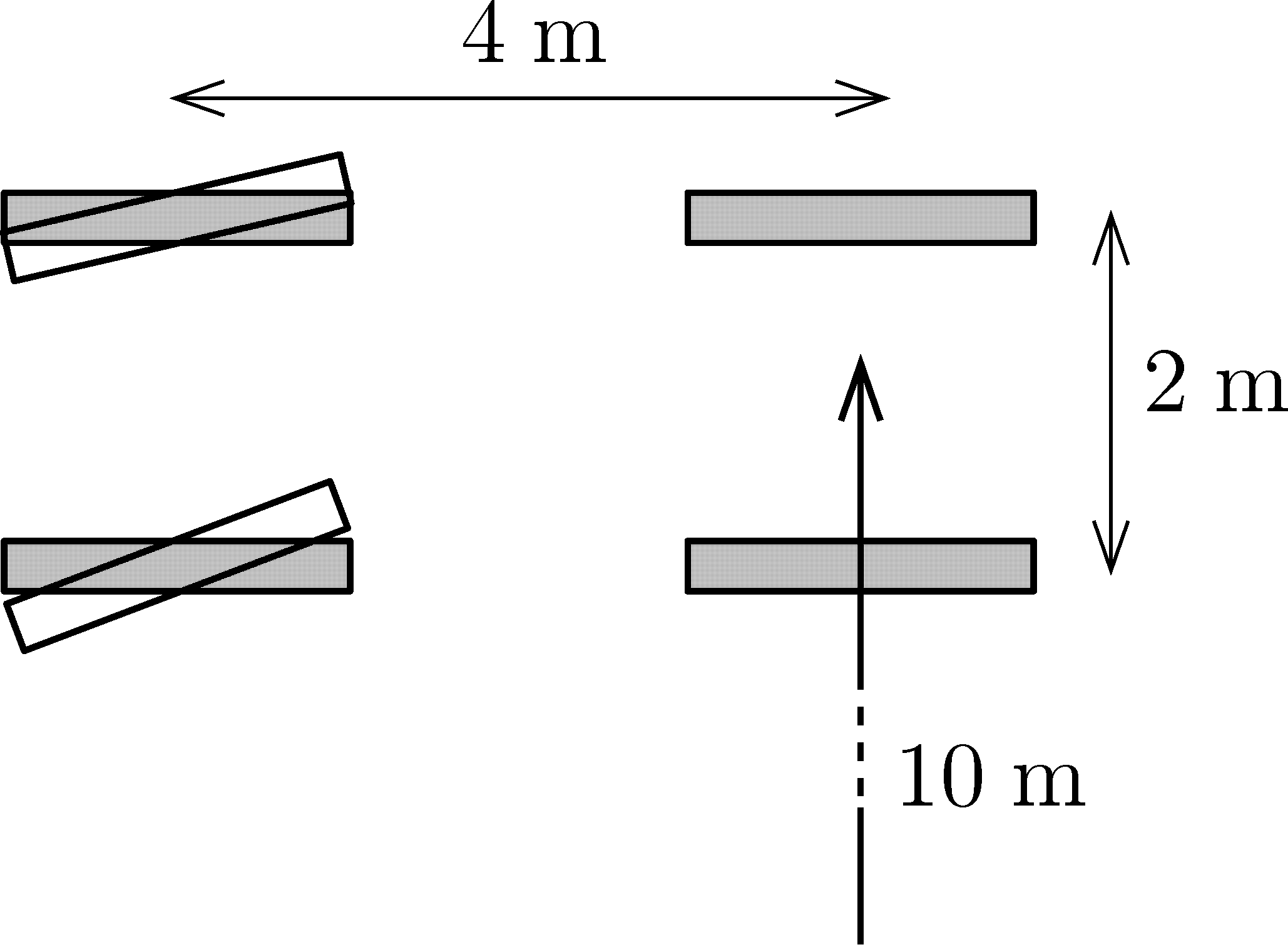
a) If the centre of the line segment between the rear wheels turns around a circle of radius \(\displaystyle R=10~\mathrm{m}\) when the car turns, what is the radius of the circles drawn by the wet wheels of the car on the dry asphalt?

b) During turning, what is the angle turned by the front wheels about the vertical axis?

(3 pont)

Deadline expired on January 15, 2025.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. a) Az autó bal hátsó kereke 9 m, a jobb hátsó kerék pedig 11 m sugarú körön fordul. Az autó tiszta rotációt végez, ezért minden pontja olyan körön mozog, aminek ugyanott van a középpontja. Pitagorasz-tétel segítségével számíthatjuk ki, hogy a bal első kerék \(\displaystyle r_1=\sqrt{9^2+4^2}\,\mathrm{m}=9{,}85\,\mathrm{m}\), míg a jobb első kerék \(\displaystyle r_2=\sqrt{11^2+4^2}\,\mathrm{m}=11{,}7\,\mathrm{m}\) sugarú körön mozog.

b) A kerekeknek úgy kell elfordulniuk, hogy síkjuk merőleges legyen a körpályájuk sugarára. Merőlegesszárú szögek alapján számíthatjuk ki a két első kerék elfordulását:

\(\displaystyle \alpha_1=\arcsin\frac{4}{9{,}85}=\arctan\frac{4}{9}=24^\circ,\)

illetve

\(\displaystyle \alpha_2=\arcsin\frac{4}{11{,}7}=\arctan\frac{4}{11}=20^\circ.\)

Megállapíthatjuk, hogy a két első kerék elfordulási szöge nem azonos (esetünkben a két szögelfordulás közti különbség \(\displaystyle 4^\circ\)), a külső körön futó kerék elfordulása a kisebb.

Megjegyzések. 1. A feladatot megoldhatjuk geometriai szerkesztéssel (körzővel, vonalzóval), majd a kérdéses sugarakat és szögeket lemérhetjük vonalzóval és szögmérővel. Ez a módszer is teljes értékű megoldásként fogadható el.

2. A valóságban a jobb útfekvés érdekében a kormányozott kerekeket nemcsak elforgatják, hanem meg is döntik.

Statistics:

24 students sent a solution.
3 points:	Békési Máté, Csáki Anikó, Hegedüs Márk, Kovács Artúr-Lehel, Kovács Tamás , Majer Veronika, Medgyesi András, Molnár Sámuel , Szighardt Anna, Szilaj Petra, Vízhányó Janka.
2 points:	Hollósi Dominik, Horváth Zsombor, Huba Zsombor .
1 point:	5 students.
0 point:	2 students.
Not shown because of missing birth date or parental permission:	1 solutions.

Problems in Physics of KöMaL, December 2024