 |
Az I/S. 52. feladat (2021. március) |
I/S. 52. Bergengóciában \(\displaystyle N\) darab város van, melyek 1-től \(\displaystyle N\)-ig számozottak. Jelenleg semelyik kettő sincs összekötve autópályával, így a király útépítési projektet hirdet. Pontosan akkor szeretné az \(\displaystyle x\) és \(\displaystyle y\) sorszámú városokat összekötni autópályával (\(\displaystyle x< y\)), ha az \(\displaystyle x\) szám osztója az \(\displaystyle y\)-nak, de nincs olyan \(\displaystyle z\) sorszám, amely osztható \(\displaystyle x\)-szel és osztója \(\displaystyle y\)-nak. Azaz, ha a szabály alapján \(\displaystyle x\) összeköthető \(\displaystyle z\)-vel és \(\displaystyle z\) összeköthető \(\displaystyle y\)-nal, akkor \(\displaystyle x\) és \(\displaystyle y\) között nem lehet út. (A várost saját magával nem kötjük össze.)
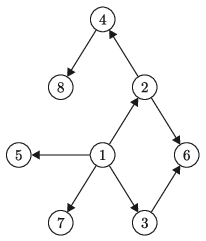
A király tanácsadójaként adjuk meg, hogy \(\displaystyle N\) város esetén hány autópályát kell építtetnie a királynak a leírt szabályok alapján.
Bemenet: az első és egyetlen sor a városok \(\displaystyle N\) számát tartalmazza.
Kimenet: a kimenet első és egyetlen sorába írjuk az építtetendő utak számát.
| Példa bemenet | Példa kimenet |
| 8 | 8 |
Korlátok: \(\displaystyle 1\le N\le 1\,000\,000\). Időkorlát: 0,4 mp.
Értékelés: A pontok 30%-a kapható, ha \(\displaystyle N< 100\). A pontok 60%-a kapható, ha \(\displaystyle N< 10\,000\).
Beküldendő egy is52.zip tömörített állományban a megfelelően dokumentált és kommentezett forrásprogram, amely tartalmazza a megoldás lépéseit, valamint megadja, hogy a program melyik fejlesztői környezetben futtatható.
(10 pont)
A beküldési határidő 2021. április 15-én LEJÁRT.
Horcsin Bálint megoldása:
Látható, hogy csak azok a megfelelő x, y párok, amelyekre \(\displaystyle \frac{y}{x}=p\) prím. Átrendezve \(\displaystyle \frac{y}{p}=x\). Vagyis ha megállapítjuk, hogy egy \(\displaystyle y\)-nnak hány egymástól páronként eltérő prím osztója van, és ezt minden \(\displaystyle y\in [2,n]\)-re összegezzük, akkor megkapjuk a feladat megoldását. De ezzel megegyezik, ha minden prímre megnézzük, hogy hány számnak osztója a \(\displaystyle [2,n]\) intervallumon. Egy adott \(\displaystyle p\) prímre ezen számok darabszáma \(\displaystyle \left\lfloor \frac{n}{p}\right\rfloor\). A prímeket Erathostenes szitájával megkereshetjük, és az eredményeket ősszegezhetjük.
Komplexitás: Erathostenes szitájának futásideje \(\displaystyle \mathcal{O}(N*log(log(N)))\), és ezen kívül csak konstans műveleteket végzünk, így a megoldás futásideje is \(\displaystyle \mathcal{O}(N*log(log(N)))\).
Statisztika:
12 dolgozat érkezett. 10 pontot kapott: Horcsin Bálint, Kovács Alex, Melján Dávid Gergő, Tóth 057 Bálint, Ürmössy Dorottya, Varga 256 Péter. 6 pontot kapott: 1 versenyző. 5 pontot kapott: 1 versenyző. 3 pontot kapott: 2 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2021. márciusi informatika feladatai

