 Problem I/S. 6. (February 2016)
Problem I/S. 6. (February 2016)
I/S. 6. We are given \(\displaystyle N\) (\(\displaystyle 1\le N\le 1000\)) towers. The height of each tower, an integer between 0 and 100 inclusive, is known. Our city is considered to be nice if the height difference of any two towers is at most 17. Our architects can modify the tower heights: increasing or decreasing the height of any tower by \(\displaystyle x\) levels costs \(\displaystyle x^2\) units of money. You should determine the minimum amount of money to make the city nice. Each tower should have a non-negative integer number of levels for all the time.
Your program should read the value of \(\displaystyle N\) from the first line of the standard input. The tower heights are found in the next \(\displaystyle N\) lines. The first and only line of the standard output should contain the minimum amount of money to complete the task.
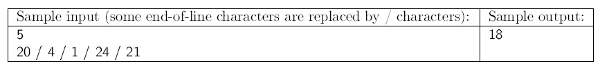
Explanation. Towers of height 4, 20 and 21 are kept; 3 new levels are added to the tower of height 1, and 3 levels are removed from the tower of height 24.
Scoring and bounds. You can get 1 point for a brief and proper documentation clearly describing your solution. Nine further points can be obtained provided that your program solves any valid input within 1 second of running time.
The source code of your program with a short documentation—also describing which developer environment to use for compiling the source—should be submitted in a compressed file is6.zip.
(10 pont)
Deadline expired on March 10, 2016.
Statistics:
19 students sent a solution. 10 points: Bálint Martin, Gergely Patrik, Hornák Bence, Janzer Orsolya Lili, Kiss Gergely, Kovács 246 Benedek, Mernyei Péter, Nagy Ábel, Németh 123 Balázs, Németh 729 Gábor, Noszály Áron, Olexó Gergely, Radnai Bálint, Vári-Kakas Andor. 5 points: 1 student. 4 points: 1 student. 2 points: 3 students.
Problems in Information Technology of KöMaL, February 2016
