 Problem I. 168. (October 2007)
Problem I. 168. (October 2007)
I. 168. We set up a wireless network in a rectangular room by installing three WiFi antennas. We know that the strength of the signal is inversely proportional to the square of the distance from the antenna, further, every computer in the room receives the signal which is the strongest at that position. For simplicity we assume that the room can be covered by squares with side length of 1 m. The computers and antennas are in the interior of these squares. The distance of two squares is defined as the minimum number of squares connecting the original two. (Hence the distance of a square from itself is one.) The signal strength computed this way is rounded to the nearest integer.
Let us consider the following example. The size of the room is 4×3 square meters, and the positions of the antennas are at (4,3) with strength of 90, at (1,1) with strength of 70, and at (1,3) with strength of 60. The corresponding coverage diagram of the room is then the following:
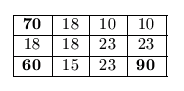
The signal strength within square (4,3) is 90, since the distance from the nearest antenna here is 1. Adjacent squares have signal strength of 23, since now the distance is 2, and is rounded to 23.
Write a program that creates a coverage diagram for a room of size of at most 25×25. The size of the room, the coordinates of the antennas and their strength are given as input to the program. The coverage diagram should be displayed on the standard output using a similar format as in the example (with values rounded to integers and each occupying 3 characters).
You should submit the source code of the program (i168.pas, i168.cpp, ...), a short documentation of your solution (i168.txt, i168.pdf, ...) and the name and version number of the compiler (e.g.,. Free Pascal 2.0, Borland C++ 3.1, ...).
(10 pont)
Deadline expired on November 15, 2007.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás
Englert Péter (11. osztály, Zalaegerszeg, Zrínyi M. Gimn.) munkája Pascal nyelven:
C++ nyelven készült mintamegoldás:
Külön szeretnénk felhívni a figyelmet a mintamegoldásra, amely sehol sem használ lebegőpontos értékeket vagy kerekítést.
Típushibák, tanulságok
A feladat a könnyebbek közé tartozott, három jellegzetes hiba legalább egyikét azonban mégis sokan elkövettétek.
Az első két hiba szinte kizárólag együtt fordult elő. Sok megoldás nem kezelte helyesen, ha egy mezőn lévő jeladó gyengébb volt, mint egy máshonnan odaérkező jel, illetve ha egy mezőn több jeladó is volt. Ahogy sokan jól észrevették, ezen úgy lehetett segíteni, hogy a jeladó(ka)t tartalmazó mezőket ugyanúgy kezeltük, mint minden más mezőt, és ugyanúgy vettük rá a 3 jeladó pontbeli erősségének maximumát, ahogy a többi mezőre is. (Ezért is volt egy mező önmagától 1 távolságra.)
Adódott probléma az osztás-kerekítés elvégzésével is. Ez abból adódott, hogy egyes nyelvek (C#), ill. fordítók (Free Pascal) kerekítésre alapesetben nem a szokványos ("away from zero") eljárást alkalmazzák, hanem a kerekítési hiba mérséklése érdekében a félúton lévő számokat a legközelebbi páros számra kerekítik ("to even"). Így pl. Turbo Pascalban round(12.5)=13 , de Free Pascalban 12.
A probléma ugyanakkor roppant elegánsan megoldható kizárólag egészekkel és maradékos osztással (div), mégpedig egészen egyszerűen úgy, hogy az osztandóhoz hozzáadjuk az osztó felét, majd ezt az összeget osztjuk. Így nyelvtől és platformtól függetlenül mindig helyes eredményt kapunk.
A feladatspecifikációban szereplő korlátokról
A feladatok szövegében gyakran találkozunk a bemenetre vonatkozó megszorításokkal, korlátokkal: pl. "N egész, (0<N 50000)", "legfeljebb 25×25-ös táblázat", "3 darab szóközzel elválasztott egész szám".
50000)", "legfeljebb 25×25-ös táblázat", "3 darab szóközzel elválasztott egész szám".
Rendkívül fontos azonban megérteni, hogy ezek a feltételek nem a programmal, hanem a felhasználóval szemben támasztanak bizonyos elvárásokat.
Gyakran találkozunk azzal a helytelen értelmezéssel, hogy - a fenti példánál maradva - a kód N értékét beolvasva azt összeveti a határokkal; ellenőrzi, hogy a terem szélessége és magassága 1 és 25 közé esik-e; a sorban valóban 3 szám szerepel-e, stb. Az ilyesfajta ellenőrzések akár több tíz, esetleg száz sor terjedelműek is lehetnek, jelentősen megnövelve a megoldás elkészítéséhez szükséges időt.
Örömmel jelenthetjük, hogy az ilyesfajta vizsgálódás nemcsak nem kötelező, hanem teljes mértékben felesleges. Attól a pillanattól kezdve ugyanis, hogy feladatspecifikációban rögzítettük a bemenetre vonatkozó korlátokat, minden ettől eltérő bemenet következményéért (rossz eredmény, végtelen ciklus...) a felhasználó felel. A specifikációt egyfajta szerződésként képzelhetjük el a program és a környezete közt: kizárólag az abban rögzített feltételek teljesülése esetén tudjuk garantálni a program helyes működését.
Természetesen komoly programoknál az első bekezdésben leírtakhoz hasonló kikötések nem szerepelhetnek a specifikációban, ott szinte kötelező, hogy a bemenet helyességét, értelmességét ellenőrizzük, a program "bolondbiztos" legyen. Ez általában rengeteg monoton, unalmas többletmunkát és -kódot eredményez.
A feladatszövegekben szereplő korlátokkal épp ettől a munkától szeretnénk megkímélni titeket, annak érdekében, hogy minden erőtökkel a feladat érdemi, kihívást jelentő, "szép" részére koncentrálhassatok. Ennek értelmében a megoldások tesztelése során mindig igazodni fogunk a specifikációhoz, így e feltételek teljesülését a program írása során tényként kezelhetitek.
A feladatkiírásban szereplő megkötések tehát - a fenti példáknál maradva - helyesen a következőképp értelmezendők:
- N biztosan egy pozitív, 50000-nél nem nagyobb egész szám, tehát nyugodtan beolvashatom egy előjel nélküli, 16 bites egész változóba, nem fog túlcsordulni. Nyugodtan oszthatok vele, nem fordulhat elő 0-val osztás.
- A táblázat számára egy fix méretű 25x25-ös tömböt foglalok, és az értékeket ebbe fogom beolvasni, legfeljebb nem használom a teljes táblázatot. A tömb túlindexelése nem fordulhat elő.
- A sor biztosan 3 darab egész számot fog tartalmazni legalább 1 szóközzel elválasztva, így formázott beolvasás esetén a 3 egész számot váró scanf/readln hívás biztosan sikeres lesz.
Ugyanakkor szeretnénk arra is felhívni figyelmeteket, hogy a specifikációt a másik oldalról is ugyanilyen szigorúan vesszük: biztosak lehettek benne, hogy a megoldásokat olyan tesztadatokkal is fogjuk ellenőrizni, melyben N értéke 1 vagy 50000; a táblázat mérete 1x1, 1x25 vagy 25x25. A teljes pontszám eléréséhez a programnak ezekben az esetekben is jól kell működnie.
Statistics:
19 students sent a solution. 10 points: Englert Péter, Fábián András, Hodosy Gábor, Horváth 135 Loránd, Kaposvári Tamás, Pap 987 Dávid, Póta Kristóf, Szpisják Dániel, Véges Márton. 9 points: Erdős Gergely, Szabó 313 Gábor. 8 points: 1 student. 7 points: 2 students. 6 points: 2 students. 5 points: 1 student. 4 points: 1 student. 0 point: 1 student.
Problems in Information Technology of KöMaL, October 2007
