Problem I. 190. (September 2008)
I. 190. We simulate the crystallization of a melted substance in a rectangle-shaped furnace. The box is divided into N×M squares, containing either 0 (melted state) or 1 (crystallized state). A square with melted substance crystallizes, if at least 3 squares out of its 8 neighbours have already crystallized. See the figure.
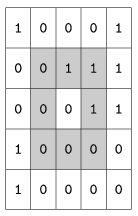
The state of each square is recomputed in every simulation step, and we change melted into crystallized state where necessary. (In the next simulation step in the example, the middle 0 will become 1, because it has at least 3 crystallized neighbours. Similarly, the fourth cell in the first row will be 1, but no more changes will take place in this step.)
The command line argument of your program is the name of the input file containing the initial pattern of crystals. The first row of the input file contains two positive integers, the number of rows (3
N200) and columns (3M200) of the state matrix. Then each of the following N lines contains M values, either 0 or 1.
The output of your program (written on the standard output) should contain the number of steps in which complete crystallization occurs. (If this does not happen, the output should be ``Crystallization has stopped''.)
See the example (``Bemenet'' is input, and ``Kimenet'' is output).
The source code of your program (i190.pas, i190.cpp, ...) together with a short documentation (i190.txt, i190.pdf, ...) should be submitted, also containing a brief description of your solution and the name of the developer environment to use.
(10 pont)
Deadline expired on October 15, 2008.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás menete:
A megoldás során két tömböt (T1 és T2) használunk a szimulációstér aktuális és következő állapotának tárolásához (lásd mintamegoldás). Az Elokeszit eljárás a folyadékot ábrázoló 0-kal veszi körbe a cellák halmazát, így a kristály szomszédok megszámlálása nem igényel külön eljárást a mátrix szélén. A folyadék 0 és a kristály 1 ábrázolása a kristály szomszédok számának meghatározását egyszerű összegzésre vezeti vissza. Elég a Szomszedszamlalas() függvényt csak a folyadék, 0 tartalmú cellák esetén használnunk. A Szimulacio eljárást addig hajtjuk végre, amíg változás történik. Ha az 1-esek, azaz kristályok száma megegyezik a cellák számával, akkor a minden folyadék kikristályosodott, különben a kristályosodás előbb leállt.
Típushibák:
Sok beküldött program a standard bemenet és kimenet használata helyett fájlból olvasta és fájlba írta az eredményt. Nagy adatmennyiségekkel így nem lehet tesztelni a megoldásokat. Nem kellett megjeleníteni minden lépés után a szimulációsteret. Ez nagy méretnél nem is lehetséges karakteres felbontásnál. A be- és kimenettel több probléma volt. Több program szóközöket várt a bemeneti adatok között, illetve a futás végén billentyűleütésre várt. Amennyiben a feladat szövegében a be- és kimenetet pontosan definiáljuk, úgy a program a bemenetet mindig a specifikált formában fogja kapni, így azt nem kell ellenőrizni, illetve a kért kimeneten kívül semmi mást nem kell kiírni.
Siegler Gábor
Megoldás:
Statistics:
25 students sent a solution. 10 points: Dévényi Attila, Englert Péter, Erdős Gergely, Fár Attila Gergő, Földes Imre, Gaizer Bence, Hunyady Márton, Jákli Gábor, Kővágó Zoltán, Molnár Gábor, Nagy 111 Miklós, Póta Kristóf, Szabó 313 Gábor, Uray Marcell János. 9 points: Pap 999 Dávid. 8 points: 3 students. 7 points: 1 student. 5 points: 2 students. 4 points: 2 students. 3 points: 1 student. 1 point: 1 student.
Problems in Information Technology of KöMaL, September 2008