Problem I. 248. (October 2010)
I. 248. There is a single continuous black curve on an N×N black and white image (the number of pixels, N is 
100). We know only the chain code of the curve and we have to recover the original image.
The chain code of a curve is briefly described in the following. The code contains the coordinates of the starting point and the successive directions obtained as we travel along the curve. The starting point is any of the endpoints of the curve. As we travel along the curve from the starting point to the other endpoint, we note the direction in each step. The figure shows the 8 possible directions.
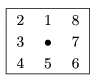
By using a spreadsheet application, you should recover the image if the chain code of the curve is known.
The sheet ,,In'' should contain the following pieces of information:
-- coordinates of the starting point
-- successive directions, so that they can be entered below each other
-- auxiliary sheets and computations needed to produce the image. You should take into account the maximal possible size of the image.
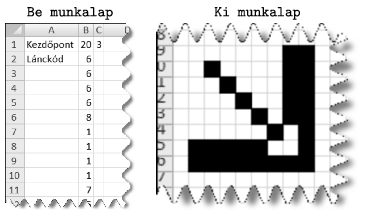
Then you should prepare a sheet ,,Out'' to display the image. You should adjust column width and row height such that cells are displayed as squares. All cells should be visible on the screen. Cells that are part of the curve can be denoted by an arbitrary character. The example shows a possible input (,,Be munkalap'') and output (,,Ki munkalap'').
Your solution may not contain macros or program modules, only formulae and built-in functions. All auxiliary computations should be visible and nothing should be hidden.
Your spreadsheet (i248.xls, i248.ods, ...) together with a short documentation (i248.txt, i248.pdf, ...) -- also describing the name and version number of the spreadsheet application, further a brief description of your solution -- should be submitted.
(10 pont)
Deadline expired on November 10, 2010.
Sorry, the solution is available only in Hungarian. Google translation
Megoldásokról
A táblázatkezelési feladat nem jelentet nehézséget a versenyzőknek. Tartalmilag mindenki jó megoldást küldött be. Sajnos a formai elvárásoknak viszont kevesen feleltek meg. A munkalapokat át kellett volna nevezni Be és Ki-re, valamint a megoldások elvét néhány mondatban kértük. Ez több versenyzőnél elmaradt.
Mintamegoldásként Gema Barnabás 10. osztályos (Veszprém, Lovassy László Gimnázium) tanuló munkáját közöljük: i248.xls
A kezdőpont koordinátái a C1 és D1 cellákba, a lánckódok pedig a B2:B12000 cellatartományba írhatjuk. A táblázat először a C és D oszlopokba, a lánckódok mellé kiszámolja a pontok koordinátáit, majd az E oszlopban összefűzi egy cellában a kettőt vesszővel elválasztva. Ezt a koordinátát kell visszakeresni egy képpont megjelenítéséhez.
Ha a bevitt adatok valamiért nem megfelelőek, akkor az A3-mas cellában figyelmeztetés jelenik meg. Hibás a bevitt adat, ha egy képpont átlépné a kép határát, vagy a lánckódok közé nem megfelelő érték kerül. A kép készítése a hibás sornál leáll. Az A4-es cellában megjelenik a megadott kódok száma. Ezt a megjelenítésnél figyelembe kell venni. A cellatartományok hivatkozási címeit az A5 és az A6 cellákba generáljuk.
Az E1:E12000 cellatartományban keressük a pontok koordinátáit. A szükséges erőforrások minimalizálásának érdekében mindig csak abban a tartományban keresünk, ahol még vannak koordináták. Ezért van szükség az A4, az A5 és az A6 cellákban lévő adatokra. Az INDEX és a HOL.VAN függvények egymásba ágyazásával kapott kereső függvény hibát jelez, ha nem találja meg a keresett cellát, ezért szükség volt egy másik függvényre is. Ez megállapítja, hogy a keresőfüggvény jelez-e hibát. Ha igen, akkor nem jelenít meg semmi, Ha nem, akkor kitölti a képpontot egy n betűvel.
A kép először csak a Be munkalapon jelenik meg, ezt másolja át a táblázat a Ki munkalapra, ahol már megfelelő méretben jelenik meg.
Statistics:
8 students sent a solution. 10 points: Barta 111 János, Gema Barnabás, Szabó 928 Attila. 9 points: Kalló Kristóf, Kovács Kornél, Leitereg András, Nánási József, Paróczi Gergő.
Problems in Information Technology of KöMaL, October 2010