 Problem I. 256. (January 2011)
Problem I. 256. (January 2011)
I. 256. Many phenomena in nature involve some kind of pattern formation, typically driven by mechanisms in which various figures emerge from the initially uniform system. Spectacular examples include chemical waves (e.g. the famous Belousov--Zhabotinsky reaction), or animal coat pattern formation.

Your program i256 should simulate pattern formation by using the following model. Initially you take an M×M (10 M
M 500) grid with each cell having two possible colors. Colors are conveniently represented in a matrix. At the beginning of the simulation, each cell has a random color. In each of the following simulation steps you can change the color of a single random cell by the majority rule: the cell will take the color that is most common within its neighborhood. You should update the color of the cell directly on the screen without redrawing the complete grid in order to avoid flickering. Of course the shape of the resulting patches depends on the size of the neighborhood K (1
500) grid with each cell having two possible colors. Colors are conveniently represented in a matrix. At the beginning of the simulation, each cell has a random color. In each of the following simulation steps you can change the color of a single random cell by the majority rule: the cell will take the color that is most common within its neighborhood. You should update the color of the cell directly on the screen without redrawing the complete grid in order to avoid flickering. Of course the shape of the resulting patches depends on the size of the neighborhood K (1 K
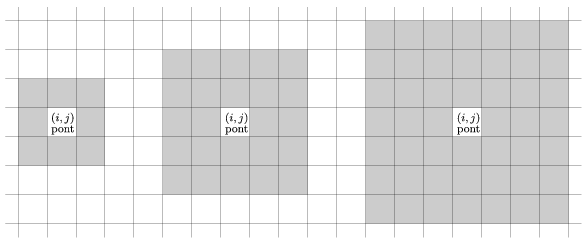
K 4) used in the majority rule. The example shows different neighborhood sizes for K=1,2 and 3. Boundary points have of course less neighboring cells. The simulation should run until the user stops it.
4) used in the majority rule. The example shows different neighborhood sizes for K=1,2 and 3. Boundary points have of course less neighboring cells. The simulation should run until the user stops it.
The command line arguments to your program are M and K. The second example shows a random initial grid together with a possible state after some simulation steps with M=150 and K=1.
 |  |
The source code (i256.pas, i256.cpp, ...) together with a short documentation (i256.txt, i256.pdf, ...) -- also describing which developer environment to use for compiling, further a brief description of your solution -- should be submitted.
(10 pont)
Deadline expired on February 10, 2011.
Sorry, the solution is available only in Hungarian. Google translation
Megoldásokról
A feladatra 9 megoldás érkezett, amelyek közül 2 volt teljes értékű. Szerencsére a többivel is ki lehetett próbálni a mintázat képződés szimulációs modelljét különböző paraméterekkel. A feladat kérte, hogy „a program parancssori argumentuma legyen M és K értéke”. Ezt a futtatási üzemmódot sajnos többen nem tartották be.
Két kép M=300 és K=4 paraméterek esetén.
Röviddel idővel az indítás után...

...kicsit később...

... és egy stabilizálódott minta.

Mintamegoldásként Seres Márk Dániel (Hódmezővásárhely, Bethlen Gábor Református Gimnázium, 11. osztály) tanuló munkáját közöljük: i256.pas
Statistics:
9 students sent a solution. 10 points: Gema Barnabás, Seres Márk Dániel. 9 points: Barta 111 János, Szabó 928 Attila, Varga 256 Erik. 8 points: 2 students. 7 points: 1 student. 5 points: 1 student.
Problems in Information Technology of KöMaL, January 2011
