 Problem I. 271. (September 2011)
Problem I. 271. (September 2011)
I. 271. In this exercise you are going to model percolation--a phenomenon when a liquid passes through a solid (but porous) substance. Your program i271should run the simulation on a grid of n×n squares (1 n
n 500), representing a vertical cross section of the solid material. The liquid can pass through each cell with probability p (0.00
500), representing a vertical cross section of the solid material. The liquid can pass through each cell with probability p (0.00 p
p 1.00), say, through a microscopic crack, and can not pass with probability 1-p.
1.00), say, through a microscopic crack, and can not pass with probability 1-p.
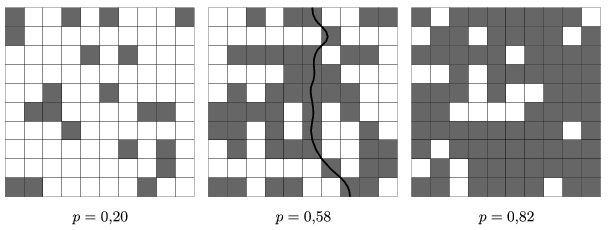
A liquid can not pass through the material in first figure in the example, but can pass from top to bottom in the second figure: darker cells allow percolation. The liquid can move from a cell to its bottom left, bottom or bottom right neighbor.
Create a statistics to count how many times the liquid could percolate through the solid material, as the parameter p is varied.
To do this, first fix an arbitrary n (between the given lower and upper bounds) -- in the documentation, this side length n should also have the same value. Then, for each p, generate at least 100 random grids and count how many times a liquid could pass through the given material. Let us call this number per. (Then, clearly, of grids with the given p.) Finally, the (p,per) pairs should be written into a text file, and displayed on a PointXY diagram using a spreadsheet application.
The source code of your program (i271.pas, i271.cpp, ...), the spreadsheet (i271.xls, i271.ods, ...) containing the diagram, further, a brief description of your solution (i271.txt, i271.pdf, ...) and the name of the developer environment to use for compiling the source file should be submitted in a compressed file i271.zip.
(10 pont)
Deadline expired on October 10, 2011.
Sorry, the solution is available only in Hungarian. Google translation
Megoldásokról
A perkoláció olyan kémiai, fizikai, geológiai jelenség, amelynél az a kérdés, hogy a repedések, anyaghibák, stb. alkotnak-e összefüggő hálózatot. Szimulációs program készítése volt a feladat, amellyel tanulmányozni, lehet egy szilárd test áteresztő képességét. A szimulációban, illetve annak specifikációjában néhány fontos szabály rögzítve volt. A szilárd anyag metszetét egy n×n-es (1 n
n 500) négyzet alakú terület ábrázolta. A folyadék csak felülről lefelé, azaz három irányba terjedhetett.
500) négyzet alakú terület ábrázolta. A folyadék csak felülről lefelé, azaz három irányba terjedhetett.
A beérkezett megoldásokról:
A négyzet n oldalhossza a megadott feltételek között tetszőleges, a statisztika készítése során rögzített. A feladatmegoldók jelentős része az átjárhatóságot rekurzív útkereséssel jól oldotta meg. Látszólag ez jó módszer, de sajnos n értékének növekedésével a futási idő rohamosan nő. Gyakorlatilag mindenkinél n=50 esetén a futási idő 1 perc fölé nő. A specifikációban szándékos választása. A bemenetet többen feleslegesen ellenőrizték. Erre vonatkozó tanácsokról itt olvashattok: stdio.pdf
Egy megoldás:
Gema Barnabás 11. évfolyamos versenyző (Veszprém, Lovassy László Gimnázium) dokumentációja alapján A program először a táblázat felső sorában az átengedő cella attribútumát megváltoztatja. Ez az új attribútum azt jelenti, hogy az adott cellán folyadék folyhat át. Ezek után a következő sorokat vizsgáljuk. Minden átengedő cellánál megnézi, hogy felette található-e olyan cella, amiből a folyadék lefolyhat. Ha igen, akkor megváltoztatja a vizsgált cella attribútumát. Ez a vizsgálat lefut a táblázat minden során. Csak abban az esetben áll meg az algoritmus, ha egy sorban nincsen olyan cella, amely átengedné a folyadékot. Az utolsó sornál a program megvizsgálja, hogy van-e olyan cella, amibe eljutott a folyadék. Ha talál ilyet, akkor az átengedő anyagok számát megnöveli eggyel. i271.pas
A szimuláció elemzése:
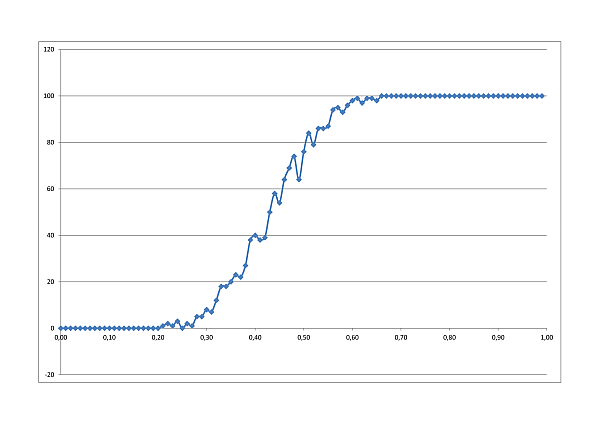
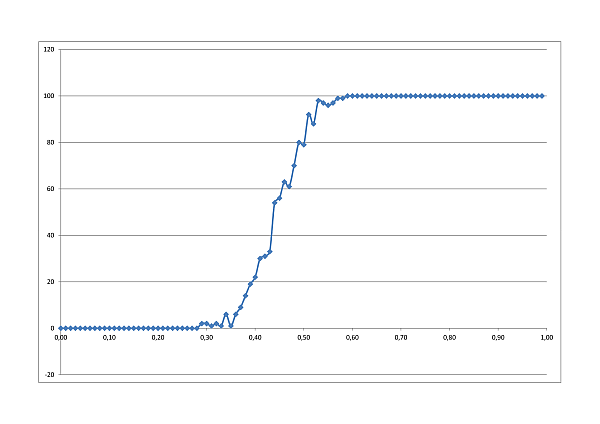
A perkolációs hálózat összefüggőségének, a szilárd anyag áteresztőképességének vizsgálatát statisztikailag vizsgálja szimulációs programunk. A táblázat minden cellája p valószínűséggel átengedi a folyadékot. Rögzített n oldalhossz mellett statisztikailag vizsgáltuk az áteresztőképesség p-től való függését. A szilárd anyag vastagságának növelésével egyre élesebb az 50%-os valószínűségnél várható váltás.
10×10 tábla esetén
20×20 tábla
100×100 tábla
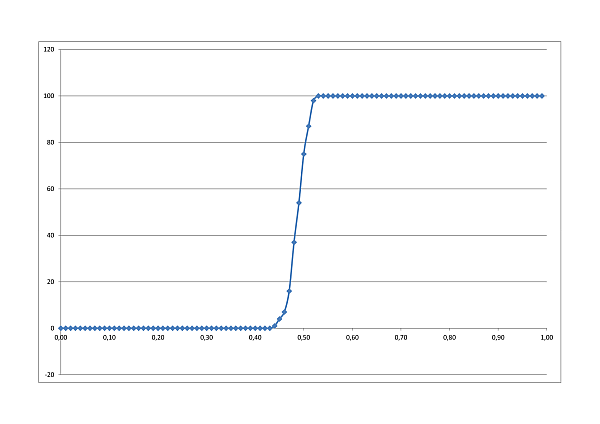
500×500 tábla
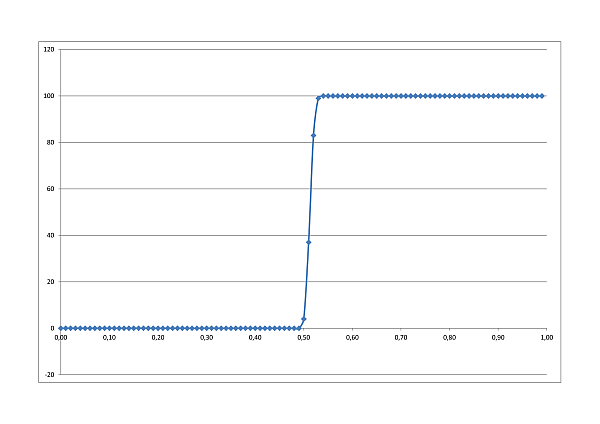
Statistics:
14 students sent a solution. 10 points: Adrián Patrik, Gema Barnabás, Hoffmann Áron, Jákli Aida Karolina. 9 points: Barkaszi Richárd Miklós, Fényes Balázs. 8 points: 5 students. 7 points: 3 students.
Problems in Information Technology of KöMaL, September 2011
