 Problem I. 298. (September 2012)
Problem I. 298. (September 2012)
I. 298. We are given an N×N billiard table with some point-like balls initially having integer coordinates within the table. When balls collide with the boundary, they are reflected in a perfectly elastic manner.
Your program i298 should determine and display on the standard output the number of ways a given ball starting from (k,l) can hit another selected ball located at (x,y).
We impose some simplifying assumptions on the path of the moving ball as follows: before hitting the target ball, it can collide with at most two walls, and it should not touch any third ball during its route. If the moving ball hits the corner of the table, then the outgoing trajectory will be the same as the incoming one and we count this as two wall collisions.
The output of your program is the number of possible paths grouped according to 2, 1 or 0 boundary collisions. The example shows 3 possible paths.
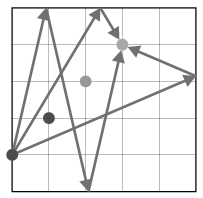
The command line input to your program is the name of the data file describing the initial conditions. The first line of the file contains the size of the board N (2 N
N 50) and the number of balls M (1<M
50) and the number of balls M (1<M 20). The next M lines describe the coordinates of the balls, then coordinates of the source ball (k,l) (1
20). The next M lines describe the coordinates of the balls, then coordinates of the source ball (k,l) (1 k,l
k,l N) and the target ball (x,y) follow. The lower left corner of the table has coordinates (1,1) and the first coordinate increases to the right, while the second one upwards.
N) and the target ball (x,y) follow. The lower left corner of the table has coordinates (1,1) and the first coordinate increases to the right, while the second one upwards.
In the table ``Bemenet'' is a sample input referring to the figure, while ``Kimenet'' is the corresponding output. ``Ket/Egy/Nulla pattanas'' gives the number of boundary collisions: 2, 1 or 0.

The source code of your program (i298.pas, i298.cpp, ...) together with a short documentation (i298.txt, i298.pdf, ...) should be submitted, also containing a brief description of your solution and specifying the name of the developer environment to use for compiling the source code.
(10 pont)
Deadline expired on October 10, 2012.
Sorry, the solution is available only in Hungarian. Google translation
Megoldásokról
Fényes Balázs 10. évfolyamos versenyző (Budapest, Szerb Antal Gimnázium) rövid értelmezése alapján:
A rajzokon a (k;l) koordinátákkal megadott golyót - vagyis amelyet elgurítunk - kék színnel jelöltem. Az (x;y) koordinátájú golyót - vagyis amelyiket el kell találnunk - pedig pirossal.
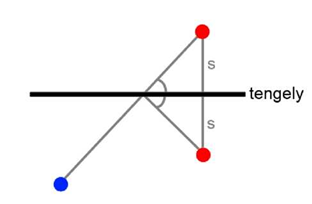
A kék golyó útvonalát könnyebben elképzelhetjük akkor, amikor a falról visszapattan, ha a piros golyót tükrözzük arra a falra, amelynek a kék golyó nekiütközött. Azaz készítünk egy tengelyes tükrözést, ahol a fal a tengely.
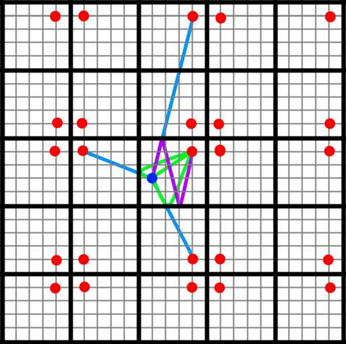
Mivel a kék golyó legfeljebb 2-szer pattanhat, ezért képzeljünk el egy 5x5 darab biliárdasztalt egymás mellé rakva az ábra szerint úgy, hogy középen van a középső asztal a kék golyót is tartalmazó eredeti; a többi asztalt úgy rakjuk le mellé, hogy a már lerakott asztalhoz képest tengelyesen tükrözött legyen, a tengely pedig az asztalok érintkező széle.
Az ábrára berajzoltam néhány lehetséges útvonalat.
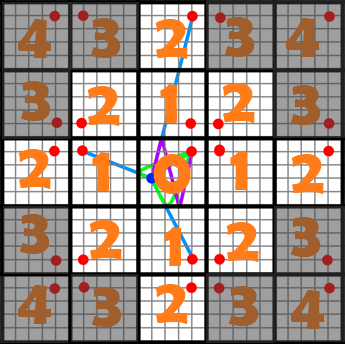
Ha megszámoljuk, hogy az egyes billiárdasztalra való eljutáshoz hányszor kell az asztalok szélén átlépni (a sarkon való átlépés 2-nek számít, mivel ott az asztal 2 széle találkozik), akkor megtudhatjuk, hogyha nincsen más golyó az asztalon, ami akadályozná a mozgását: 1 db pattanás nélküli út, 4 db egypattanásos út, 8 db kétpattanásos út lehetséges legfeljebb. Legyen a bal alsó asztal a (x = -2;y = -2) koordinátájú. Nem kell megvizsgálni, hogy az adott asztalra elgurulhat-e a kék golyó, ha az asztal koordinátáira igaz, hogy: |x| + |y|<2
A (0;0) koordinátájú asztalhoz képest vízszintes tengely mentén tükrözöttek az olyan asztalok, melyek koordinátájának y értéke páratlan, és függőleges tengely mentén tükrözöttek az olyan asztalok, melyek koordinátájának x értéke páratlan.
Ha azt vizsgáljuk, hogy az (a;b) asztal piros golyóját el lehet-e találni a (0;0) kék golyójával, akkor megnézem a (0;0), (0;b), (a;b), (a;0) asztalok által meghatározott téglalap mindegyik asztalát.
Ellenőrzéskor kiszámoljuk az induló-, és célpont által meghatározott egyenes függvényének hozzárendelési szabályát. Majd a két pont közti egész x koordinátákról eldönti, hogy behelyettesítve, rácsponton megy-e át.
Mintamegoldás:
Fényes Balázs 10. évfolyamos tanuló (Budapest, Szerb Antal Gimnázium) i298.cs
Gema Barnabás 12. évfolyamos tanuló (Veszprém, Lovassy László Gimnázium) i298.pas
Jákli Aida Karolina 10. évfolyamos tanuló (Zalaegerszeg, Zrínyi Miklós Gimnázium) Module1.vb
Statistics:
11 students sent a solution. 10 points: Fényes Balázs, Gema Barnabás, Jákli Aida Karolina. 9 points: Dobos-Kovács Mihály, Németh 017 András, Qian Lívia, Tegzes Tamás. 7 points: 1 student. 5 points: 1 student. 3 points: 1 student. 2 points: 1 student.
Problems in Information Technology of KöMaL, September 2012
