 Problem I. 337. (January 2014)
Problem I. 337. (January 2014)
I. 337. Jenga is a popular game requiring some physical skills. The rules of the game (in Hungarian) can be found at http://tarsasoznijo.blog.hu/2009/04/14/jenga. By giving up some excitement of the original game and focusing on the logic, Jenga can also be played online at http://hu.freeonlinegames.com/game/jenga.
Unlike in the classical game, we now build a tower of n levels as a starting step. When viewing from the top, successive levels have the following alternating A or B structure (see the figure).

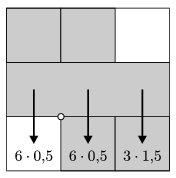
To investigate whether the tower collapses or not, each Jenga element is decomposed into three identical square-based prisms with each prism having unit weight (hence in this form the structural differences between different tower levels would disappear). The tower above an incomplete level can collapse, so let us consider the supporting edge where the tower elements and the missing ones meet. The tower collapses if the torque on the ``missing side'' of the supporting edge is greater than the torque on the other side. Let us illustrate and explain this in more detail by analyzing an example. In the figure showing a side view of a portion of the tower, the lowest level on the left has a missing Jenga element and the supporting edge is denoted by a small circle. In the computations, each element is replaced by a mass point located at the center of mass of the element; in the example we assume that the middle level has no missing Jenga elements. The torque on the missing side is 3 units (= weight × lever arm length = 6×0.5), while the torque on the other side is 7.5 units (the weight above the middle column is 6 units with arm length of 0.5 units, and the weight above the right column is 3 units with arm length of 1.5 units). Consequently, the tower in the example will not collapse.
Your program should determine the step in which the tower collapses by examining the sequence of movements of the Jenga elements. The first line of the input contains the number of levels. Then each of the following lines describes a movement by 3 numbers: the first number specifies the level number from which the element is taken, the second number (1, 2 or 3) specifies the position of this element within the level, and the third number (again 1, 2 or 3) gives the position of the element on the topmost level it is placed. The output should contain the critical step number in which the collapse occurs, and the reason of the collapse: either because of removing the element (``az eltávolítás miatt'') or because of placing the element on the top (``az elhelyezés miatt'').
In the example, ``Bemenet'' is input, and ``Kimenet'' is the corresponding output.

The first and second command line arguments to your program are the name of the input and output files, respectively.
The source code (i337.pas, i337.cpp, ...) together with a short documentation (i337.txt, i337.pdf, ...), containing a brief description of your solution and also specifying the developer environment to use for compiling the source, should be submitted in a compressed file (i337.zip).
(10 pont)
Deadline expired on February 10, 2014.
Sorry, the solution is available only in Hungarian. Google translation
A feladat kevés versenyzőt vonzott és csak két teljesen helyes megoldás született.
A feladat megoldását megkönnyítette - volna - a játékszabály is, amely szerint csak teljes emelet alól lehet kivenni elemet és az, hogy csak teljes emeletek építhetők. Mivel az elemek itt abszolút pontossággal, súrlódásmentesen mozgathatók - szemben a valósággal, a probléma arra egyszerűsödhet, hogy azon az emeleten, ahonnan az elemet kivesszük, hány elem maradt és hol.
A két legjobban sikerült megoldás Fényes Balázsé (i337fenyes.cs) és Kovács Balázs Marcellé ( i337kovacs.cpp).
Az értékelés során a dokumentáció 2 pontot ért. Az előírásoknak megfelelő program 1 pontot jelentett. A tesztesetekre (i337teszt.zip) helyes megoldásonként 0,5-0,5 pont volt szerezhető.
Statistics:
5 students sent a solution. 10 points: Fényes Balázs, Kovács Balázs Marcell. 7 points: 1 student. 3 points: 1 student. 0 point: 1 student.
Problems in Information Technology of KöMaL, January 2014
