 Problem I. 394. (February 2016)
Problem I. 394. (February 2016)
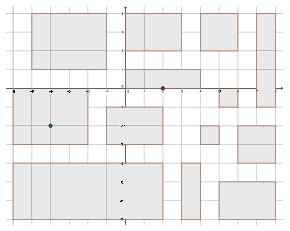
I. 394. An imperial probe droid is searching for rebels in the city of Nhalo. The buildings in the city are rectangular, and the corresponding sides are parallel to one another. The probe droid starts its mission in a given building; it scans the entire building, then proceeds to the closest building which is the smallest. Its algorithm is described more precisely below.
The time to scan a building is equal to the area of the building. After the droid has finished scanning a building, it considers the closest unvisited buildings and picks one of the smallest. If there are more smallest buildings, the droid chooses the one having the smallest \(\displaystyle X\) coordinate. If there are equal \(\displaystyle X\) coordinates, it chooses the building with the smallest \(\displaystyle Y\) coordinate. The time needed for the droid to move from one building to another is negligible. The distance between two buildings is defined by the smallest distance between any two of their respective points.
The rebels are currently hiding in a given building. They know the algorithm of the droid, and also the building the droid starts its search from. The rebels immediately start the evacuation, but they need to know how much time they have: they should leave before the droid finds their building.
Your program reads the city map and the starting positions of the rebels and the droid from the standard input (A discussion about handling the standard I/O can be found, for example, in the file stdio.pdf, downloadable from our web page, after the solution of the problem S.64.).
The first line of the input contains a positive integer representing the number of buildings \(\displaystyle P\) (\(\displaystyle 2\le P\le 100\)). The next \(\displaystyle P\) lines of the input contain the coordinates of the buildings (each coordinate is an integer between \(\displaystyle -100\) and \(\displaystyle +100\)). The next-to-last line of the input contains the starting position of the droid, while the last line of the input contains the coordinates of a point of the rebel building. The first line of the standard output should contain the available time for the rebels for the evacuation. The second line of the output should contain the time for the droid to scan the individual buildings before it finds them.
Example (with newline characters replaced by / characters):
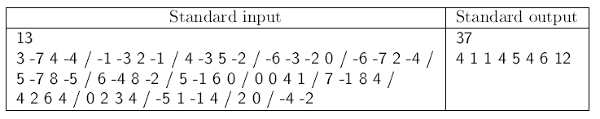
The source code and a short documentation of your program—containing a brief description of your solution, and the name of the developer environment to compile your code—should be submitted in a compressed file i394.zip.
(10 pont)
Deadline expired on March 10, 2016.
Statistics:
5 students sent a solution. 10 points: Hamrik Szabin, Kovács 246 Benedek, Nagy Ábel, Olexó Gergely. 7 points: 1 student.
Problems in Information Technology of KöMaL, February 2016
