 |
Az I. 486. feladat (2019. május) |
I. 486. Monte Carlo városában két egyenrangú út keresztezi egymást. A város vezetése azon gondolkodik, hogy a kereszteződést körforgalommá építse át. Az átépítést abban az esetben végeznék el, ha az autók átlagos áthaladási ideje a körforgalomban kisebb lenne, mint a kereszteződésben. Készítsünk programot, amely adott közlekedési viszonyok mellett megadja a kereszteződés és a körforgalom esetén az átlagos áthaladási időt!
A város autósai különösen udvarias emberek, akik a következő szabályok betartásával közlekednek:
1. a kereszteződésben, illetve a körfogalomban mindig az érkezés sorrendjében történik az áthaladás;
2. ha több autó egyszerre érkezik, akkor az kezdheti meg az áthaladást, akinek az a legkevesebb ideig tart; ha több ilyen jármű is van, akkor a jobbkéz-szabály alapján kezdik meg az áthaladást; ha mindegyik jármű ilyen, akkor véletlenszerűen választanak egyet, és ő kezdi meg az áthaladást, majd azután alkalmazzák a jobbkéz-szabályt;
3. két autó egyszerre is beléphet a kereszteződésbe abban az esetben, ha útjuk nem keresztezi egymást;
4. a körforgalomban haladó járműnek elsőbbsége van az oda belépni akaró járműhöz képest.
A feladatban tekintsünk minden autót egyforma hosszúságúnak, valamint feltételezzük, hogy azonos sebességgel haladnak. Mozgásukat úgy értelmezzük, hogy egységnyi idő alatt az ábrán látható négyzetháló egy cellájából a haladásnak megfelelő, oldalával szomszédos cellába lépnek át, ha az a cella üres (vagyis nem áll ott autó, vagy az ott álló autó tovább tud lépni a cellába belépő autóval egy időben).
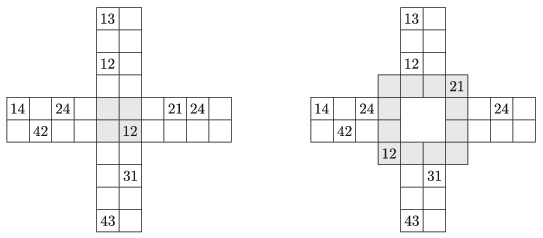
A kereszteződés és a körforgalom négyzethálós felbontása az ábra szerint történjen. A példában a négy csatlakozó útszakaszt az óramutató járása szerint az 1, 2, 3, 4 számok, az autókat kétjegyű számok jelölik: a tízesek helyén annak az útszakasznak a sorszáma van, ahonnan érkezik, az egyesek helyén ahová tart az autó.
A szimulációs programban az útszakaszok \(\displaystyle L\) hosszúak legyenek, tehát egy útszakaszon sávonként \(\displaystyle L\) négyzet csatlakozzon a kereszteződéshez, illetve a körforgalomhoz. Minden esetben összesen \(\displaystyle N\) számú autóval induljon a szimuláció, melyek mindegyike a kereszteződés, illetve a körforgalom felé tart. Az autók egyike sem fordul vissza, tehát mindegyik egy másik útszakaszon halad tovább. A program adja meg, hogy \(\displaystyle S\) számú szimuláció esetén mennyi az átlagos áthaladási idő. Ez az idő egyenlő egy-egy autó esetén a kereszteződés vagy körforgalom miatti várakozás és áthaladás idejével, tehát attól az időegységtől kezdődik, amikor az autó várakozni kényszerül a bevezető úton, vagy várakozás nélkül belép a kereszteződésbe, illetve körforgalomba, és akkor ér véget, amikor onnan kilép. Így egy 1-es útszakaszról a 4-es útszakaszba tartó, jobbra kanyarodó autó a kereszteződés esetén legkevesebb 2, a körforgalom esetén legkevesebb 4 időegység alatt halad át.
A program a standard bemenetről olvassa be \(\displaystyle L\), \(\displaystyle N\) és \(\displaystyle S\) értékét, majd a standard kimenet egy sorába írja az átlagos áthaladási időket a kereszteződés és körforgalom esetén. Korlátok: \(\displaystyle 10\le L\le 100\), \(\displaystyle L\le N< 4L\), \(\displaystyle 100\le S\le 10000\).
Beküldendő egy i486.zip tömörített állományban a program forráskódja és a hozzá kapcsolódó dokumentáció. Utóbbi a problémamegoldás lényeges elemeire világít rá, valamint tartalmazza, hogy a forrásállomány melyik fejlesztő környezetben fordítható.
(10 pont)
A beküldési határidő 2019. június 11-én LEJÁRT.
Mintamegoldásként Nagy Márton Váci, 11. évfolyamos tanuló munkáját mutatjuk be: i486.pdf, Program.cs.
Statisztika:
2 dolgozat érkezett. 10 pontot kapott: Nagy 793 Márton. 3 pontot kapott: 1 versenyző.
A KöMaL 2019. májusi informatika feladatai

