Problem K/C. 827. (October 2024)

K/C. 827. Each angle of a hexagon is \(\displaystyle 120^{\circ}\). Prove that the sum of the lengths of any two adjacent sides equals the sum of the lengths of the two adjacent sides opposite them.

(5 pont)

Deadline expired on November 11, 2024.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Mivel a hatszög minden szöge \(\displaystyle 120^{\circ}\), ezért a szemközti oldalai párhuzamosak.

Jelölje a hatszög csúcsait \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\), \(\displaystyle D\), \(\displaystyle E\) és \(\displaystyle F\) az ábrán látható módon.

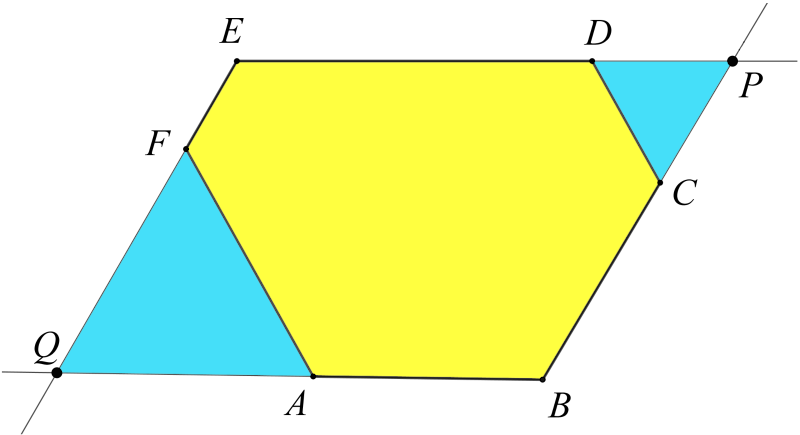
Az \(\displaystyle ED\) és a \(\displaystyle BC\) félegyenesek metszéspontját jelölje \(\displaystyle P\), az \(\displaystyle EF\) és \(\displaystyle BA\) félegyenesekét \(\displaystyle Q\). Mivel az \(\displaystyle EQBP\) négyszög szemközti oldalai párhuzamosak, így az paralelogramma, tehát a szemközti oldalai egyenlőek. Például \(\displaystyle QB=PE\), vagyis

Mivel az \(\displaystyle FQA\) és \(\displaystyle CPD\) háromszögek minden szöge 60°, ezért ezek szabályos háromszögek. Következésképp az egyes háromszögekben minden oldal egyenlő, például \(\displaystyle QA=AF\) és \(\displaystyle CD=PD\). E két egyenlőség és (1) alapján \(\displaystyle FA+AB\)=\(\displaystyle CD+DE\), vagyis erre a négy oldalra teljesül a feladat állítása. Mivel ez a gondolatmenet bármely 2-2 szemben fekvő oldalra érvényes, így a feladat állítása igaz.

Statistics:

271 students sent a solution.
5 points:	110 students.
4 points:	20 students.
3 points:	14 students.
2 points:	26 students.
1 point:	44 students.
0 point:	16 students.
Not shown because of missing birth date or parental permission:	34 solutions.

Problems in Mathematics of KöMaL, October 2024