Problem K/C. 843. (January 2025)

K/C. 843. Let \(\displaystyle ABC\) be an isosceles right triangle. Let \(\displaystyle D\) be a point on the extension of leg \(\displaystyle AB\) beyond \(\displaystyle B\) satisfying \(\displaystyle BD=AB\). Let \(\displaystyle E\) denote the midpoint of leg \(\displaystyle AC\), and let line segment \(\displaystyle ED\) intersect hypotenuse \(\displaystyle BC\) in \(\displaystyle F\). Find the ratio of the areas of triangles \(\displaystyle AED\) and \(\displaystyle FEC\).

(5 pont)

Deadline expired on February 10, 2025.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Tekintsük az ábrát. Jelölje \(\displaystyle AB\) hosszát \(\displaystyle a\).

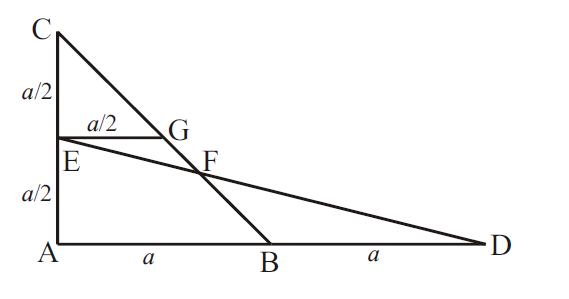
Az AED derékszögű háromszög területe: \(\displaystyle \frac12\cdot 2a\cdot\frac a2=\frac{a^2}{2}\). Az \(\displaystyle FEC\) háromszög területét két háromszög területéből tudjuk összetenni: \(\displaystyle CEG\) és \(\displaystyle EGF\) háromszögek, ahol \(\displaystyle G\) a \(\displaystyle BC\) felezőpontja. \(\displaystyle EG = \frac a2\), mert a \(\displaystyle CEG\) háromszög derékszögű, egyenlő szárú háromszög. Az \(\displaystyle EGF\) háromszög feleaakkora, mint az \(\displaystyle FBD\) háromszög, mert megfelelő oldalaik párhuzamosak, és \(\displaystyle EG\) hossza a \(\displaystyle BD\) hosszának felével egyenlő. Emiatt \(\displaystyle GF\) feleakkora, mint \(\displaystyle MF\), vagyis \(\displaystyle F\) a \(\displaystyle BG\) szakasz harmadolópontja. Emiatt az \(\displaystyle EGF\) háromszög \(\displaystyle EG\)-hez tartozó magassága \(\displaystyle \frac a2\) harmadrészével egyenlő. Tehát az \(\displaystyle FEC\) háromszög területe: \(\displaystyle \frac12\cdot\frac a2\cdot\frac a2+\frac12\cdot\frac a2\cdot\frac a6=\frac{3a^2}{24}+\frac{a^2}{24}=\frac{a^2}{6}\).

Tehát \(\displaystyle AED\) és \(\displaystyle FEC\) háromszögek területének aránya 3:1.

Statistics:

174 students sent a solution.
5 points:	90 students.
4 points:	23 students.
3 points:	6 students.
2 points:	6 students.
1 point:	11 students.
0 point:	3 students.
Unfair, not evaluated:	5 solutionss.
Not shown because of missing birth date or parental permission:	24 solutions.

Problems in Mathematics of KöMaL, January 2025