Problem K/C. 848. (February 2025)

K/C. 848. Trapezoid \(\displaystyle ABCD\) is inscribed in a circle with radius 10 such that \(\displaystyle AB\) is the diameter of the circle and \(\displaystyle \angle ABC=75^{\circ}\). Calculate the area of trapezoid \(\displaystyle ABCD\).

(5 pont)

Deadline expired on March 10, 2025.

Sorry, the solution is available only in Hungarian. Google translation

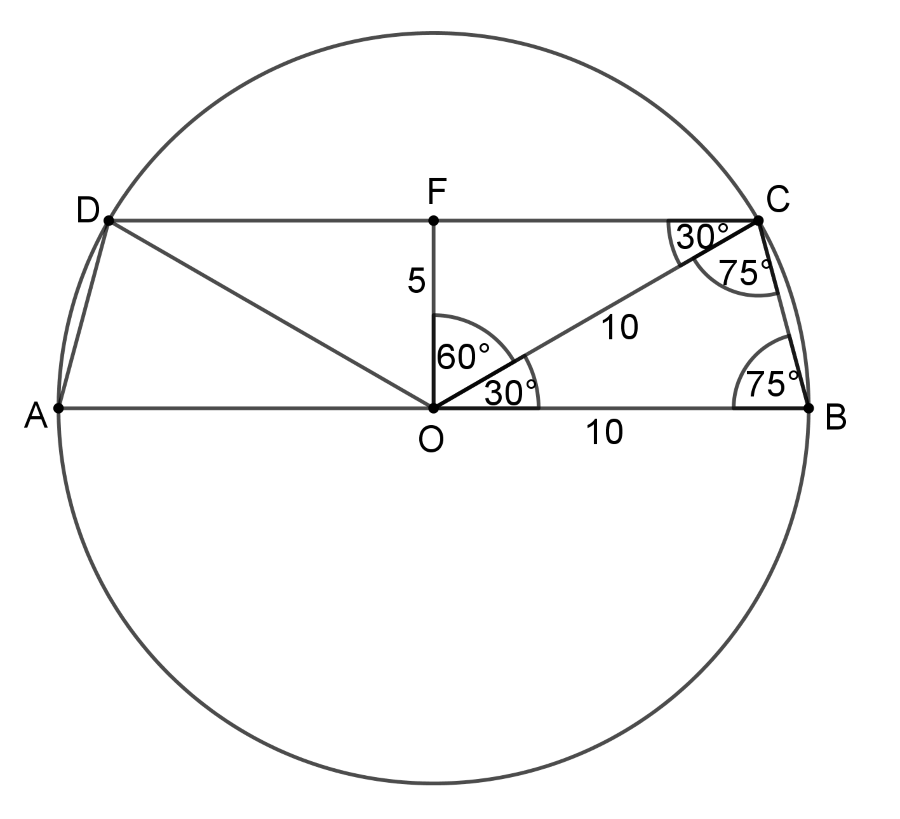
Megoldás. Az \(\displaystyle ABCD\) húrtrapéz, tehát szárai egyenlő hosszúak. Megfelelő szögeit kiszámolva az ábrán látható értékeket kapjuk. Mivel az \(\displaystyle OFC\) háromszög egy szabályos háromszög fele, és \(\displaystyle OC\) a kör sugara, ezért \(\displaystyle OC = r = 10\) cm, emiatt \(\displaystyle OF = 5\) cm, a Pitagorasz-tételből pedig \(\displaystyle FC = 5\sqrt3\) cm adódik. A trapéz területét a \(\displaystyle \frac{20+10\sqrt3}{2}\cdot5=50+25\sqrt3\) cm\(\displaystyle ^2\) összefüggés adja meg.

Statistics:

195 students sent a solution.
5 points:	105 students.
4 points:	23 students.
3 points:	14 students.
2 points:	12 students.
1 point:	1 student.
0 point:	3 students.
Not shown because of missing birth date or parental permission:	29 solutions.

Problems in Mathematics of KöMaL, February 2025