 Problem K/C. 858. (April 2025)
Problem K/C. 858. (April 2025)
K/C. 858. We drew four small blue squares in a \(\displaystyle 4\times 1\) rectangle according to the diagram

Find the ratio of the area of a single blue square and the \(\displaystyle 4\times 1\) rectangle.
Proposed by: Bálint Bíró, Eger
(5 pont)
Deadline expired on May 12, 2025.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. A \(\displaystyle 4 \times 1\)-es téglalap néhány csúcsát és a legfelső kis kék négyzet két csúcsát megjelöltük a következő ábrának megfelelően.
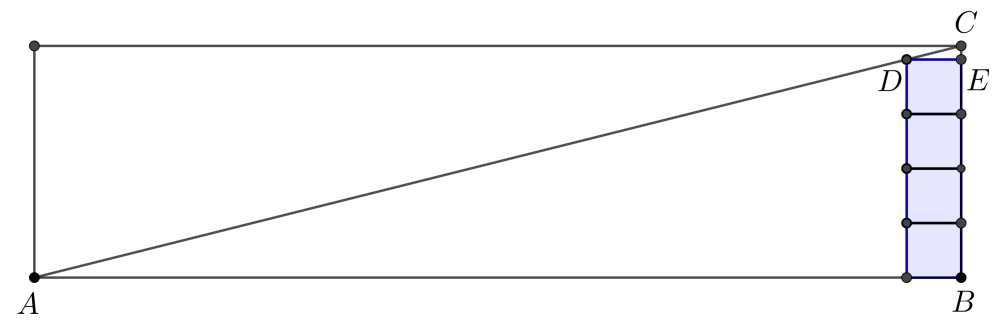
Az \(\displaystyle ABC\) és \(\displaystyle DEC\) háromszögek szögei a megfelelő oldalak párhuzamossága miatt egyenlő nagyságúak, tehát ez a két háromszög hasonló, azaz a megfelelő oldalak aránya egyenlő. Ezért a \(\displaystyle CE=x\) és \(\displaystyle DE=y\) jelöléssel
\(\displaystyle \displaystyle{\frac{x}{y}=\frac{1}{4}},\)
ahonnan
| \(\displaystyle (1)\) | \(\displaystyle y=4x\) |
következik. Ugyanakkor \(\displaystyle CB=CE+EB=x+4y=1\), tehát (1) alapján \(\displaystyle 17x=1\), ezért \(\displaystyle \displaystyle{x=\frac{1}{17}}\), és így
| \(\displaystyle (2)\) | \(\displaystyle \displaystyle{y=\frac{4}{17}}.\) |
Egy kis kék négyzet területe \(\displaystyle t=y^2\), vagyis (2) szerint \(\displaystyle \displaystyle{t=\frac{16}{289}}\), mivel pedig a \(\displaystyle 4 \times 1\)-es téglalap területe \(\displaystyle T=4\), ezért
\(\displaystyle \displaystyle{\frac{t}{T}=\frac{16}{289\cdot 4}=\frac{4}{289}},\)
tehát egy kis kék négyzet területe a \(\displaystyle 4 \times 1\)-es téglalap területének \(\displaystyle \displaystyle{\frac{4}{289}}\)-ed része.
Statistics:
155 students sent a solution. 5 points: 61 students. 4 points: 42 students. 3 points: 12 students. 1 point: 1 student. 0 point: 7 students. Unfair, not evaluated: 5 solutionss. Not shown because of missing birth date or parental permission: 21 solutions.
Problems in Mathematics of KöMaL, April 2025
