Problem K/C. 872. (October 2025)

K/C. 872. Fill in the parts denoted by \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle \ldots\), \(\displaystyle g\) of the diagram with numbers 1, 2, 3, 4, 5, 6 and 7 such that the numbers in the three circles have the same sum, and \(\displaystyle a\) is perfect square. Find all solutions.

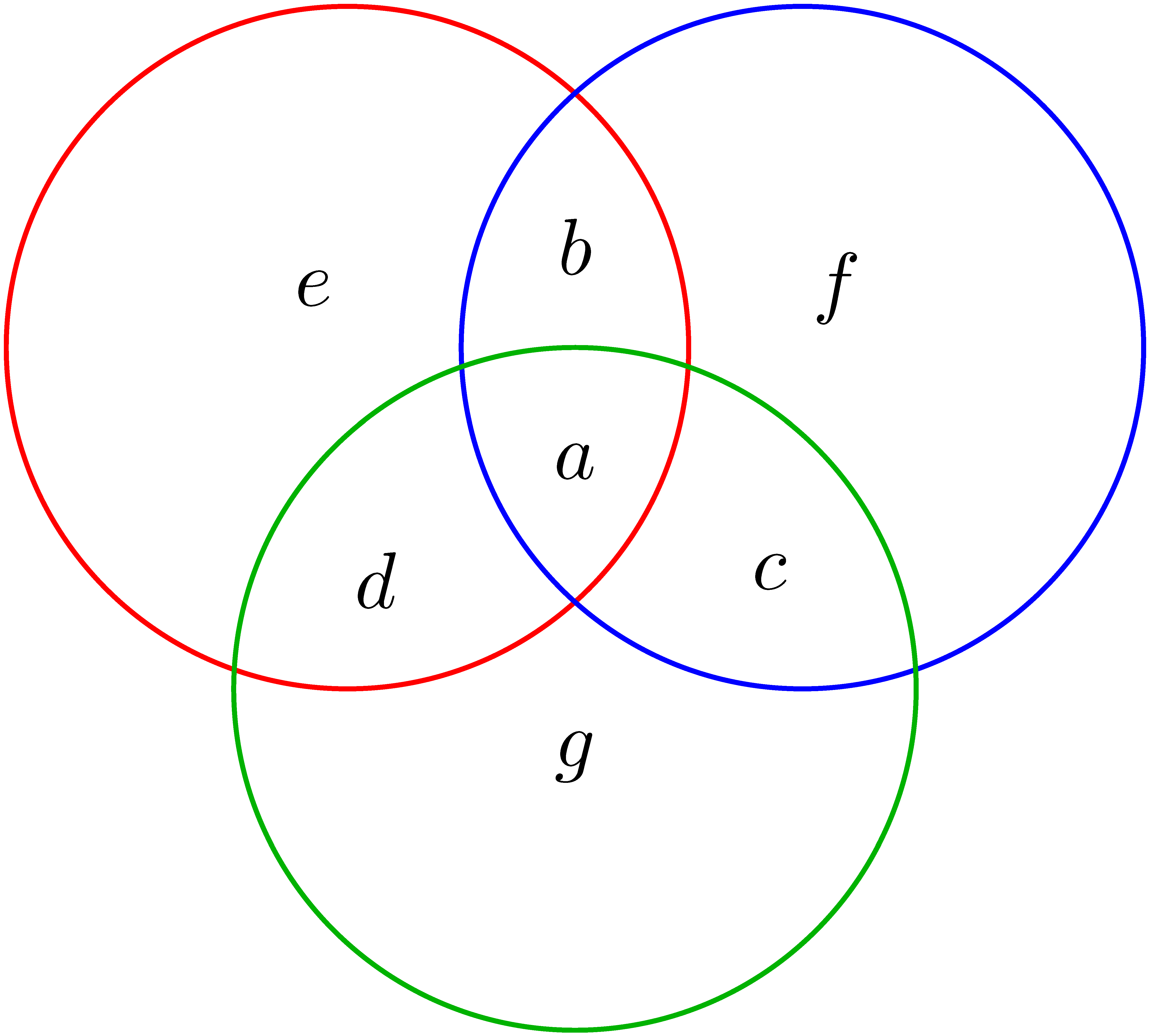
(5 pont)

Deadline expired on November 10, 2025.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. A három körben a számok összege pontosan akkor ugyanannyi (bármely két kör közös számait is figyelembevéve), ha:

\(\displaystyle e+d = f+c,\)

\(\displaystyle b+f = d+g,\)

\(\displaystyle g+c = e+b.\)

Először legyen középen az 1, és legyen a 7 egy nem átfedett körrészben, pl. \(\displaystyle e=7\). Ekkor \(\displaystyle b=2\), \(\displaystyle 3\), \(\displaystyle 4\) lehet, mert \(\displaystyle b=5\), 6 esetén \(\displaystyle e+b\) túl nagy, amivel \(\displaystyle g+c\) nem lehet egyenlő. \(\displaystyle b=2\) esetén a maradék négy szám elhelyezésére – figyelembe véve a fenti egyenlőségeket – két elrendezés adódik. Ezeknél az összeg 13 és 14 lehet. \(\displaystyle b=3\), illetve \(\displaystyle b=4\) eset nem ad lényegesen eltérő új elrendezést.

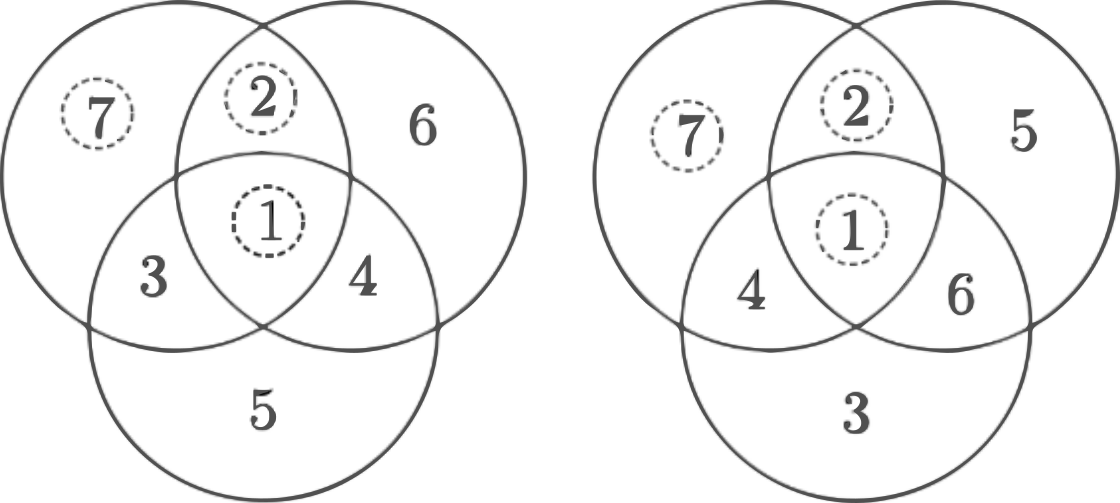
Legyen a 7-es egy két kör által lefedett részben, pl. \(\displaystyle b=7\). Ekkor \(\displaystyle e=5\) vagy 6 nem lehet, az \(\displaystyle e=2\), \(\displaystyle 3\), \(\displaystyle 4\) esetet megnézve két lényegesen különböző elrendezés adódik. Ezeknél az összeg 16 és 15 lehet.

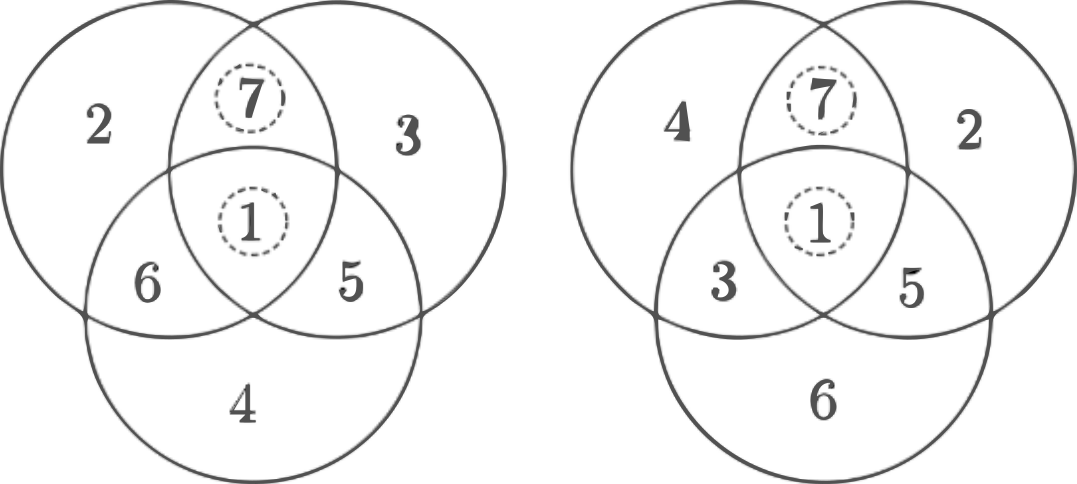
Ha a 4 van középen hasonlóképpen végignézve két különböző kitöltést kapunk, melyekben az összeg 14 és 18.

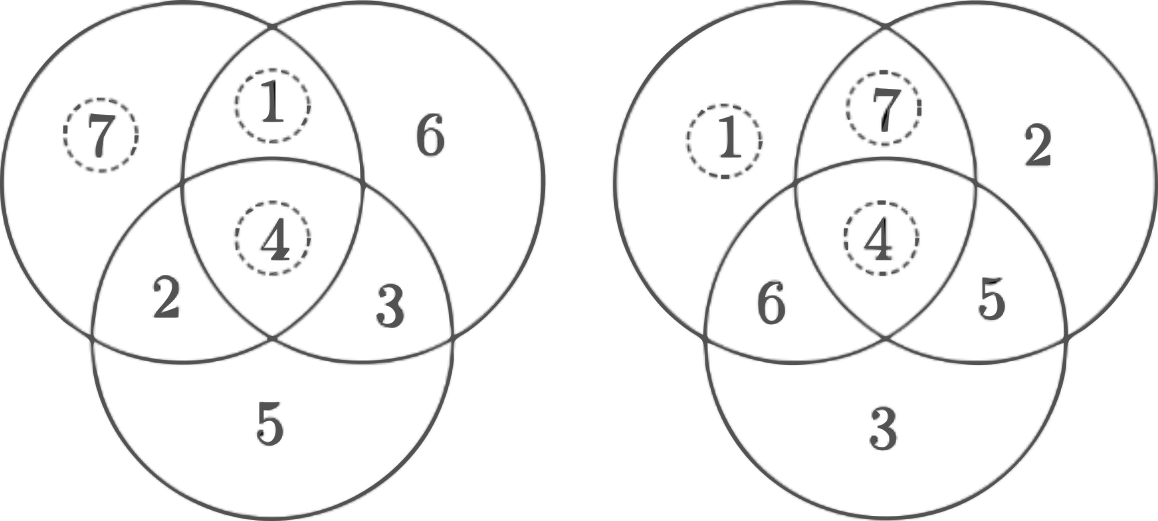
A keresett összeg 13, 14, 15, 16 és 18 lehet, és 6 különböző kitöltést találtunk.

Statistics:

Problem K/C. 872. is not processed yet.

Problems in Mathematics of KöMaL, October 2025