A K/C. 713. feladat (2021. december)

K/C. 713. Egy 6 cm oldalhosszúságú négyzet oldalaira – mint átmérőkre – egy-egy kört rajzoltunk, majd a négyzet középpontja körül megszerkesztettük azt a kört, melynek a sugara a négyzet oldalával egyenlő. Három síkrészt jelöltünk az ábrán (I., II., III.). Számítsuk ki az I., II. és III. részek területét.

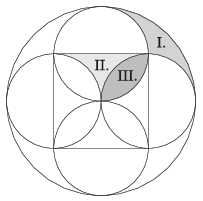
(5 pont)

A beküldési határidő 2022. január 10-én LEJÁRT.

Megoldás. A kis kör sugara 3 cm, a nagy kör sugara 6 cm. A kis kör területe 9\(\displaystyle \pi\textrm{ cm}^2\), a nagy kör területe 36\(\displaystyle \pi\textrm{ cm}^2\), a négyzet területe 36\(\displaystyle \textrm{ cm}^2\).

A négyzet területét négy félkör úgy fedi le, hogy a III. résznyi területből négyet duplán fed, így a III. rész területe: \(\displaystyle (4 \cdot 0,5 \cdot 9\pi - 36) : 4 \textrm{ cm}^2= 4,5\pi - 9 (\approx 5,14)\textrm{ cm}^2\).

A négy kis kör együttes területe megegyezik a nagy kör területével, így az általuk lefedett síkrész a négy III. résznyi átfedés miatt éppen a négy a III. résznyi területtel kisebb a nagy kör területénél. Ez a különbség megegyezik négy I. résznyi területtel is. Így a III. és az I. rész területe egyenlő.

Két darab II. rész területét megkapjuk, ha például a négyzet területéből elveszünk két félkörnyi területet, így a II. rész területe: \(\displaystyle (36 - 2\cdot 0,5 \cdot 9\pi) : 2 \textrm{ cm}^2= 18 - 4,5\pi (\approx 3,86)\textrm{ cm}^2.\)

Statisztika:

220 dolgozat érkezett.
5 pontot kapott:	161 versenyző.
4 pontot kapott:	6 versenyző.
3 pontot kapott:	18 versenyző.
2 pontot kapott:	5 versenyző.
1 pontot kapott:	5 versenyző.
0 pontot kapott:	1 versenyző.
Nem versenyszerű:	9 dolgozat.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	3 dolgozat.

A KöMaL 2021. decemberi matematika feladatai