Problem K/C. 713. (December 2021)

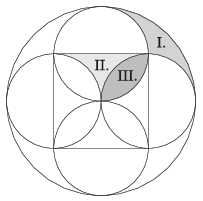
K/C. 713. The sides of a square are 6 cm long. A circle is drawn over each side as diameter, as shown in the figure. The large circle is centred at the centre of the square and its radius equals the side of the square. Calculate the areas of the regions I., II. and III.

(5 pont)

Deadline expired on January 10, 2022.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. A kis kör sugara 3 cm, a nagy kör sugara 6 cm. A kis kör területe 9\(\displaystyle \pi\textrm{ cm}^2\), a nagy kör területe 36\(\displaystyle \pi\textrm{ cm}^2\), a négyzet területe 36\(\displaystyle \textrm{ cm}^2\).

A négyzet területét négy félkör úgy fedi le, hogy a III. résznyi területből négyet duplán fed, így a III. rész területe: \(\displaystyle (4 \cdot 0,5 \cdot 9\pi - 36) : 4 \textrm{ cm}^2= 4,5\pi - 9 (\approx 5,14)\textrm{ cm}^2\).

A négy kis kör együttes területe megegyezik a nagy kör területével, így az általuk lefedett síkrész a négy III. résznyi átfedés miatt éppen a négy a III. résznyi területtel kisebb a nagy kör területénél. Ez a különbség megegyezik négy I. résznyi területtel is. Így a III. és az I. rész területe egyenlő.

Két darab II. rész területét megkapjuk, ha például a négyzet területéből elveszünk két félkörnyi területet, így a II. rész területe: \(\displaystyle (36 - 2\cdot 0,5 \cdot 9\pi) : 2 \textrm{ cm}^2= 18 - 4,5\pi (\approx 3,86)\textrm{ cm}^2.\)

Statistics:

220 students sent a solution.
5 points:	161 students.
4 points:	6 students.
3 points:	18 students.
2 points:	5 students.
1 point:	5 students.
0 point:	1 student.
Unfair, not evaluated:	9 solutionss.
Not shown because of missing birth date or parental permission:	3 solutions.

Problems in Mathematics of KöMaL, December 2021