A K/C. 717. feladat (2022. január)

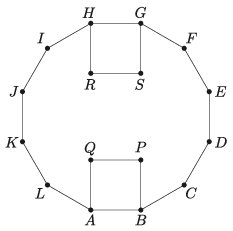
K/C. 717. Egy szabályos

\(\displaystyle ABCDEFGHIJKL \)

tizenkétszög \(\displaystyle AB\) és \(\displaystyle GH\) oldalára az \(\displaystyle ABPQ\) és \(\displaystyle GHRS\) négyzeteket írjuk befelé az ábrán látható módon. Mutassuk meg, hogy \(\displaystyle PQ\) és \(\displaystyle RS\) egy szabályos hatszög két szemközti oldala.

(5 pont)

A beküldési határidő 2022. február 10-én LEJÁRT.

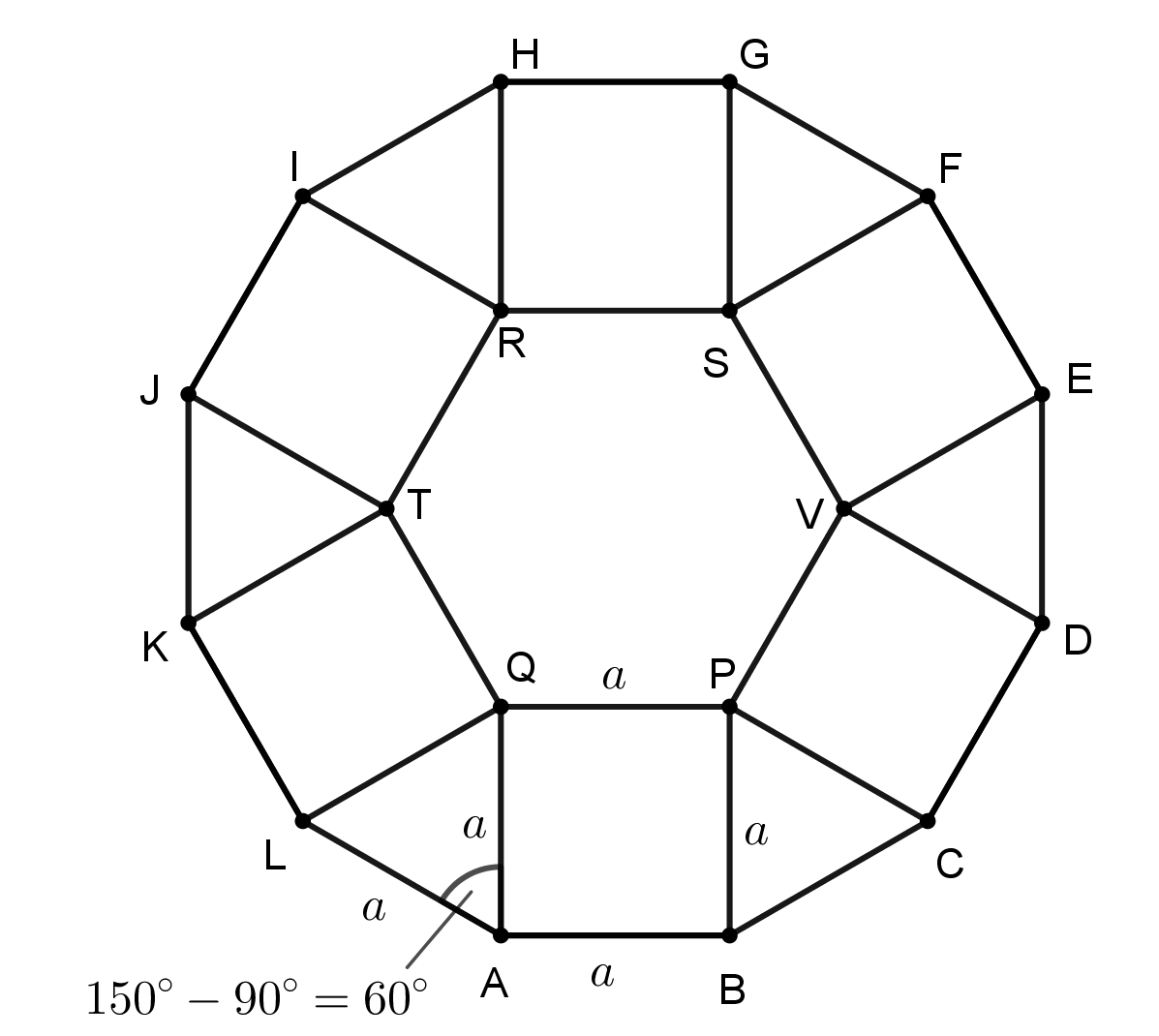
Megoldás. A szabályos tizenkétszög minden szöge \(\displaystyle \frac{10\cdot180^{\circ}}{12}=150^{\circ}\)-os.

Az eredeti ábrán az \(\displaystyle LAQ\) háromszög szabályos, mert \(\displaystyle LA=QA\) és \(\displaystyle LAQ\angle=150^{\circ}-90^{\circ}=60^{\circ}\).

\(\displaystyle KLQ\angle=150^{\circ}-60^{\circ}=90^{\circ}\), így a \(\displaystyle KL\) oldalra befelé írt négyzet harmadik csúcsa \(\displaystyle Q\) (negyedik csúcsát jelölje \(\displaystyle T\)).

\(\displaystyle PQT\angle=360^{\circ}-90^{\circ}-60^{\circ}-90^{\circ}=120^{\circ}\), és \(\displaystyle PQ=QT\).

Hasonlóképpen tovább haladva kapjuk, hogy \(\displaystyle TR=RS\), és \(\displaystyle QTR\angle=120^{\circ}\).

Szimmetrikusan kapjuk a \(\displaystyle V\) pontot is, így a \(\displaystyle QPVSRT\) hatszögről beláttuk, hogy minden oldala egyenlő hosszú és a szögei \(\displaystyle 120^{\circ}\)-osak, tehát szabályos hatszög.

Statisztika:

161 dolgozat érkezett.
5 pontot kapott:	Baksa Anna, Balog Benedek, Baráth Borbála, Bencze Mátyás, Berényi-Sima Lajos, Bettesch Emma Léda, Bettesch Helga Adél, Böröczky András Bálint, Deményi Zalán, Fehér Eszter, Fehérvári Donát, Fodor Dóra, Garamszegi Hanna, Gaspari Márton Samu, Haskó Emma, Horváth 221 Zsóka, Inokai Ádám, Iván Máté Domonkos, Jármai Roland, Juhász Emma, Kerekes András, Klement Tamás, Körmöndi Márk, Lupkovics Lilla, Mező Levente, Nagy 292 Korina, Németh Bernát, Petrányi Lilla, Pocsay Levente László, Pulka Gergely Tamás, Rási Bence, Sándor Eszter, Seprődi Barnabás Bendegúz, Sütő Áron, Téglás Dorka, Ujpál Bálint, Végh Lilian.
4 pontot kapott:	44 versenyző.
3 pontot kapott:	30 versenyző.
2 pontot kapott:	14 versenyző.
1 pontot kapott:	6 versenyző.
0 pontot kapott:	5 versenyző.
Nem versenyszerű:	11 dolgozat.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	1 dolgozat.

A KöMaL 2022. januári matematika feladatai