 Problem K/C. 743. (November 2022)
Problem K/C. 743. (November 2022)
K/C. 743. The midpoint of side \(\displaystyle BC\) of a rectangle \(\displaystyle ABCD\) is \(\displaystyle E\), and \(\displaystyle F\) is the point lying closer to \(\displaystyle D\) which divides side \(\displaystyle CD\) in a \(\displaystyle 2:1\) ratio. The midpoint of line segment \(\displaystyle AE\) is \(\displaystyle G\), and \(\displaystyle H\) is the point lying closer to \(\displaystyle E\) which divides line segment \(\displaystyle EF\) in a \(\displaystyle 2:1\) ratio. What fraction is the area of triangle \(\displaystyle FGH\) of the area of rectangle \(\displaystyle ABCD\)?
(5 pont)
Deadline expired on December 12, 2022.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Az \(\displaystyle ABCD\) téglalap oldalai \(\displaystyle AB=CD=a\) és \(\displaystyle BC=DA=b\), a téglalap területét jelöljük \(\displaystyle T\)-vel.
Jelöléseink a következő ábrán láthatók.
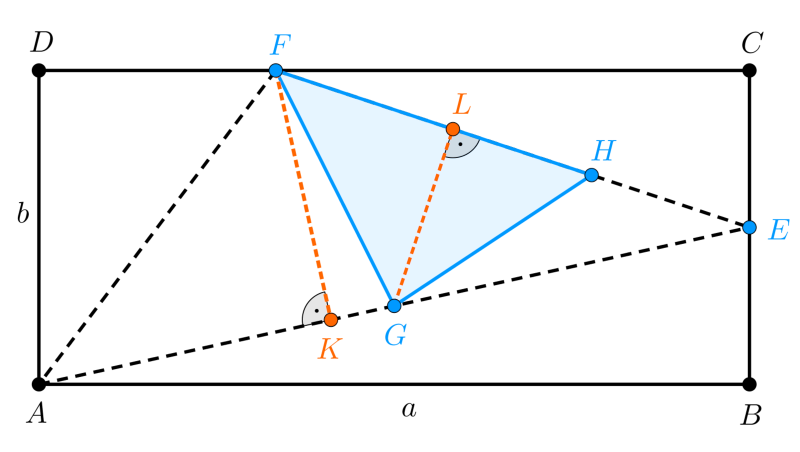
Mivel \(\displaystyle \displaystyle{T=a\cdot{b}}\) és \(\displaystyle \displaystyle{T_{ABE}=\frac{a\cdot{\frac{b}{2}}}{2}=\frac{a\cdot{b}}{4}=\frac{T}{4}}\), valamint \(\displaystyle \displaystyle{T_{ECF}=\frac{\frac{b}{2}\cdot{\frac{2a}{3}}}{2}=\frac{a\cdot{b}}{6}=\frac{T}{6}}\), továbbá \(\displaystyle \displaystyle{T_{FDA}=\frac{\frac{a}{3}\cdot{b}}{2}=\frac{a\cdot{b}}{6}=\frac{T}{6}}\), ezért
| \(\displaystyle (1)\) | \(\displaystyle \displaystyle{T_{AEF}=T-\frac{T}{4}-2\cdot{\frac{T}{6}}=\frac{5T}{12}}.\) |
Az \(\displaystyle AEF\) háromszögben \(\displaystyle FG\) súlyvonal, ez felezi az \(\displaystyle AEF\) háromszög területét (hiszen \(\displaystyle \displaystyle{T_{EFG}=\frac{EG\cdot{FK}}{2}}\), illetve \(\displaystyle \displaystyle{T_{AFG}=\frac{AG\cdot{FK}}{2}}\) és \(\displaystyle EG=AG\)).
Ezt figyelembe véve (1) szerint
| \(\displaystyle (2)\) | \(\displaystyle \displaystyle{T_{EFG}=\frac{5T}{24}}.\) |
A \(\displaystyle GH\) szakasz harmadolja az \(\displaystyle EFG\) háromszög területét, hiszen \(\displaystyle \displaystyle{T_{EGH}=\frac{EH\cdot{GL}}{2}}\), illetve \(\displaystyle \displaystyle{T_{FGH}=\frac{FH\cdot{GL}}{2}}\) és tudjuk, hogy \(\displaystyle \displaystyle{\frac{EH}{FH}=\frac{1}{2}}\).
Ebből a (2) összefüggést is felhasználva azt kapjuk, hogy
\(\displaystyle \displaystyle{T_{FGH}=\frac{2}{3}T_{EFG}=\frac{5T}{36}},\)
tehát az \(\displaystyle FGH\) háromszög területe az \(\displaystyle ABCD\) téglalap területének \(\displaystyle \displaystyle{\frac{5}{36}}\)-od része.
Statistics:
215 students sent a solution. 5 points: 109 students. 4 points: 29 students. 3 points: 23 students. 2 points: 11 students. 1 point: 9 students. 0 point: 8 students. Unfair, not evaluated: 17 solutionss. Not shown because of missing birth date or parental permission: 5 solutions.
Problems in Mathematics of KöMaL, November 2022
