Problem K/C. 753. (January 2023)

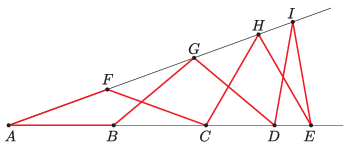
K/C. 753. Points \(\displaystyle B\), \(\displaystyle C\), \(\displaystyle D\) and \(\displaystyle E\) lie on one arm of an angle of vertex \(\displaystyle A\), and points \(\displaystyle F\), \(\displaystyle G\), \(\displaystyle H\) and \(\displaystyle I\) lie on the other arm. Given that \(\displaystyle AB=BG=GD=DI=IE=EH=HC=CF=FA\) (see the figure), show that the triangles \(\displaystyle CEH\) and \(\displaystyle IGD\) are equilateral.

(5 pont)

Deadline expired on February 10, 2023.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Jelöljük az \(\displaystyle A\) csúcsnál levő szöget \(\displaystyle \alpha\)-val. Az \(\displaystyle ACF\) egyenlő szárú háromszög \(\displaystyle C\)-nél levő belső szöge is \(\displaystyle \alpha\), ezért \(\displaystyle AFC\sphericalangle=180^{\circ}-2\alpha\).

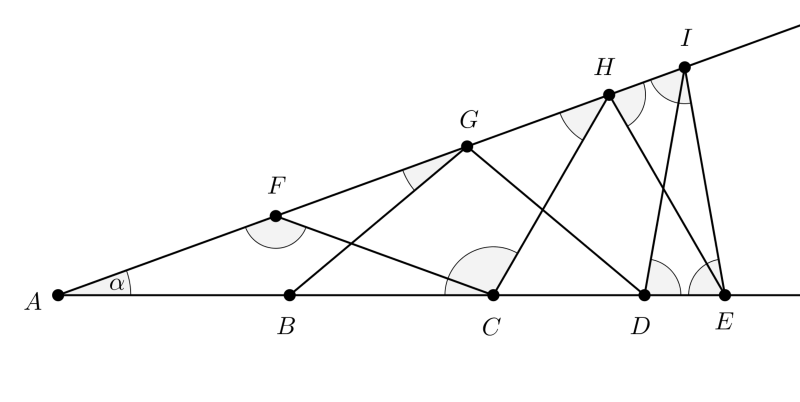
A \(\displaystyle HFC\sphericalangle=2\alpha\), mivel ez a szög az \(\displaystyle ACF\) háromszög külső szöge, és így az \(\displaystyle FHC\) egyenlő szárú háromszögben \(\displaystyle FHC\sphericalangle=2\alpha\), illetve

\(\displaystyle FCH\sphericalangle=180^{\circ}-4\alpha.\)

\(\displaystyle ECH\sphericalangle=3\alpha\), mert ez a szög az \(\displaystyle ACH\) háromszög külső szöge. Innen azonnal következik, hogy a \(\displaystyle CEH\) egyenlő szárú háromszögben \(\displaystyle CEH\sphericalangle=3\alpha\) és \(\displaystyle EHC\sphericalangle=180^{\circ}-6\alpha\).

Ebből és \(\displaystyle FHC\sphericalangle=2\alpha\)-ból következően az \(\displaystyle IHE\) egyenlő szárú háromszögben

\(\displaystyle IHE\sphericalangle=HIE\sphericalangle=4\alpha.\)

A \(\displaystyle BDG\) egyenlő szárú háromszögben \(\displaystyle DBG\sphericalangle=2\alpha\), mert ez a szög az \(\displaystyle AGB\) egyenlő szárú háromszög külső szöge, ezért \(\displaystyle BDG\sphericalangle=2\alpha\) és \(\displaystyle DGB\sphericalangle=180^{\circ}-4\alpha\) is teljesül.

Az \(\displaystyle AGB\) egyenlő szárú háromszögben \(\displaystyle BGA\sphericalangle=\alpha\), tehát \(\displaystyle DGB\sphericalangle+BGA\sphericalangle=180^{\circ}-3\alpha\), de akkor \(\displaystyle DGI\sphericalangle=3\alpha\), ennek következményeként pedig a \(\displaystyle IGD\) egyenlő szárú háromszögben \(\displaystyle DIG\sphericalangle=3\alpha\) is igaz.

Mivel előbb már beláttuk, hogy \(\displaystyle HIE\sphericalangle=4\alpha\), ezért előző eredményünkből

\(\displaystyle DIE\sphericalangle=\alpha\)

következik. Ebből adódik a \(\displaystyle DEI\) háromszögben, hogy \(\displaystyle EDI\sphericalangle=4\alpha\), hiszen ez a szög \(\displaystyle ADI\) háromszög külső szöge.

A \(\displaystyle DEI\) egyenlő szárú háromszög, ez azt jelenti, hogy

\(\displaystyle DEI\sphericalangle=4\alpha\)

is igaz. A \(\displaystyle DEI\) háromszög szögeinek összege tehát \(\displaystyle 4\alpha+4\alpha+\alpha=9\alpha=180^{\circ}\), ahonnan

\(\displaystyle \alpha=20^{\circ}.\)

A \(\displaystyle CEH\) egyenlő szárú háromszögben tehát \(\displaystyle CEH\sphericalangle=ECH\sphericalangle=3\alpha=60^{\circ}\), és így a háromszög \(\displaystyle H\) csúcshoz tartozó belső szöge is \(\displaystyle 60^{\circ}\)-os, vagyis a háromszög valóban szabályos.

Az \(\displaystyle IGD\) egyenlő szárú háromszögben pedig \(\displaystyle DIG\sphericalangle=DGI\sphericalangle=3\alpha=60^{\circ}\), eszerint ebben a háromszögben a \(\displaystyle D\) csúcsnál \(\displaystyle 60^{\circ}\)-os belső szög van, ezért ez is szabályos háromszög.

Megjegyzés.

Könnyen bizonyítható, hogy az ábra az \(\displaystyle IAE\sphericalangle=\alpha\) szög szögfelezőjére szimmetrikus.

Statistics:

160 students sent a solution.
5 points:	105 students.
4 points:	17 students.
3 points:	10 students.
2 points:	2 students.
1 point:	3 students.
0 point:	9 students.
Unfair, not evaluated:	10 solutionss.
Not shown because of missing birth date or parental permission:	2 solutions.

Problems in Mathematics of KöMaL, January 2023