 Problem K/C. 763. (March 2023)
Problem K/C. 763. (March 2023)
K/C. 763. Two squares are drawn in a semicircle of unit radius such that they both lie along the diameter, they have another side along a common line, and each has a vertex on the arc of the semicircle (see the figure).

Given that the radii drawn from the centre of the circle to the vertices lying on the circular arc are perpendicular, prove that the sum of the areas of two squares drawn in this way is constant.
(5 pont)
Deadline expired on April 11, 2023.
Sorry, the solution is available only in Hungarian. Google translation
1. megoldás. A négyzeteknek a félkörön levő csúcsait \(\displaystyle P\)-vel és \(\displaystyle Q\)-val jelöltük, ezeknek a pontoknak a félkör átmérőjére eső merőleges vetületei \(\displaystyle S\), illetve \(\displaystyle T\). A \(\displaystyle PS\) és \(\displaystyle QT\) szakaszok a négyzetek oldalai, ezeket \(\displaystyle a\)-val és \(\displaystyle b\)-vel, a kör középpontját \(\displaystyle K\)-val jelöltük.
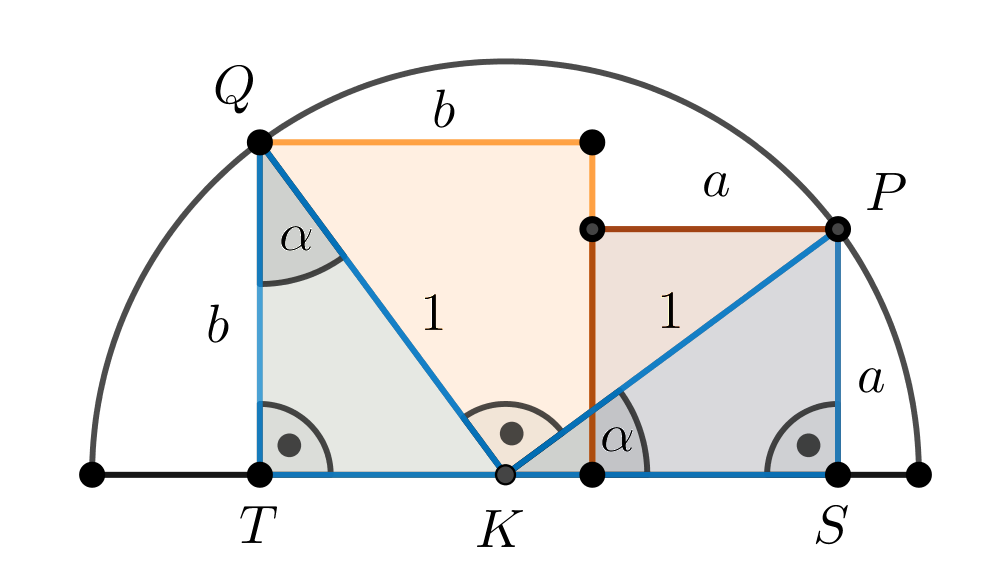
1. ábra
A feladat megadja, hogy a két négyzetnek a félkörön lévő csúcsaihoz húzott sugarak egymásra merőlegesek. Az ábrán keletkező \(\displaystyle KPS\) és \(\displaystyle KQT\) derékszögű háromszögeknek a \(\displaystyle K\) csúcsnál levő hegyesszögei \(\displaystyle \alpha\) és \(\displaystyle 90^{\circ}-\alpha\), így a két háromszög hasonló, és egyúttal egybevágó is, mert átfogójukra teljesül, hogy \(\displaystyle KP=KQ=1\). Ezért a befogóik rendre megegyeznek, azaz \(\displaystyle KS=b\) és \(\displaystyle KT=a\).
Így a Pitagorasz-tétel szerint
\(\displaystyle a^2+b^2=1.\)
A feltételeknek megfelelő négyzetek területének összege tehát valóban állandó és éppen a félkör egységnyi sugarának négyzetével egyenlő.
2. megoldás. Az 1. megoldás ábráját a \(\displaystyle KS=x\), illetve \(\displaystyle KT=y\) jelölésekkel egészítjük ki az alábbi ábra szerint.
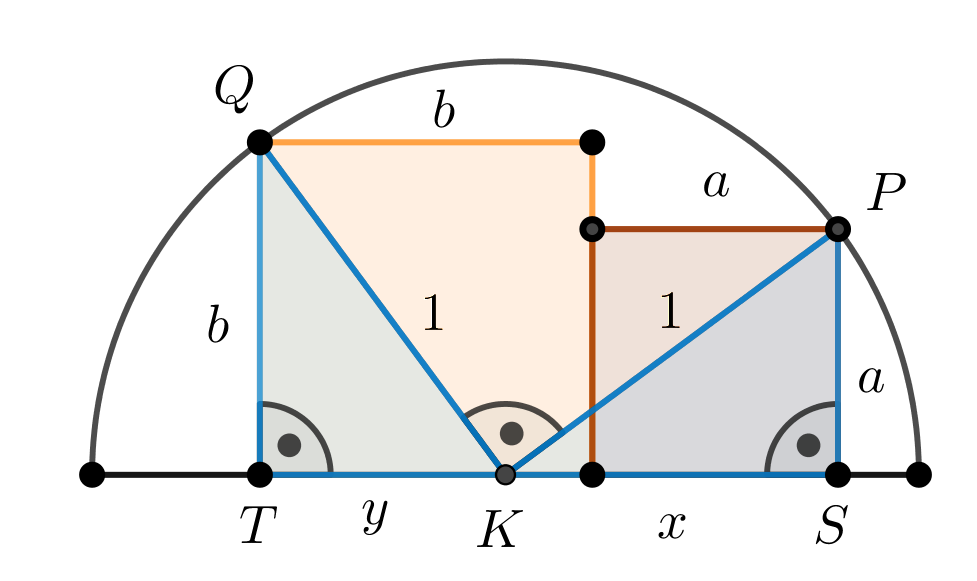
2. ábra
Írjuk fel a Pitagorasz-tételt a \(\displaystyle KPS\) és \(\displaystyle KQT\) derékszögű háromszögekre (az átfogó mindkét háromszögben a félkör egységnyi sugarával egyenlő hosszúságú):
\(\displaystyle a^2+x^2=1,\)
\(\displaystyle b^2+y^2=1.\)
Tudjuk még, hogy
\(\displaystyle x+y=a+b,\)
és így
\(\displaystyle a^2+x^2=b^2+y^2,\)
\(\displaystyle a^2-b^2=y^2-x^2,\)
\(\displaystyle (a+b)(a-b)=(y+x)(y-x).\)
Innen az \(\displaystyle x+y=a+b\) alapján egyrészt
\(\displaystyle a-b=y-x,\)
másrészt az \(\displaystyle a-b=y-x\) és \(\displaystyle a+b=x+y\) megfelelő oldalait összeadva
\(\displaystyle 2a=2y,\)
ahonnan \(\displaystyle a=y\) és ezért \(\displaystyle b=x\) adódik.
Ebből az következik, hogy a két derékszögű háromszög egybevágó, a Pitagorasz-tételt felírva tehát
\(\displaystyle a^2+b^2=1.\)
Ezzel beláttuk, hogy a két négyzet területének összege állandó, és ez az állandó a félkör egységnyi sugarának négyzete.
3. megoldás. A négyzetek félkörön levő pontjait most is \(\displaystyle P\)-vel és \(\displaystyle Q\)-val, a megfelelő négyzetek oldalait \(\displaystyle a\)-val és \(\displaystyle b\)-vel, a félkör középpontját \(\displaystyle K\)-val jelöljük. Tükrözzük a félkört és a négyzeteket a félkör átmérőjének egyenesére, a \(\displaystyle P\) és \(\displaystyle Q\) pont tükörképei legyenek \(\displaystyle P'\), illetve \(\displaystyle Q'\).
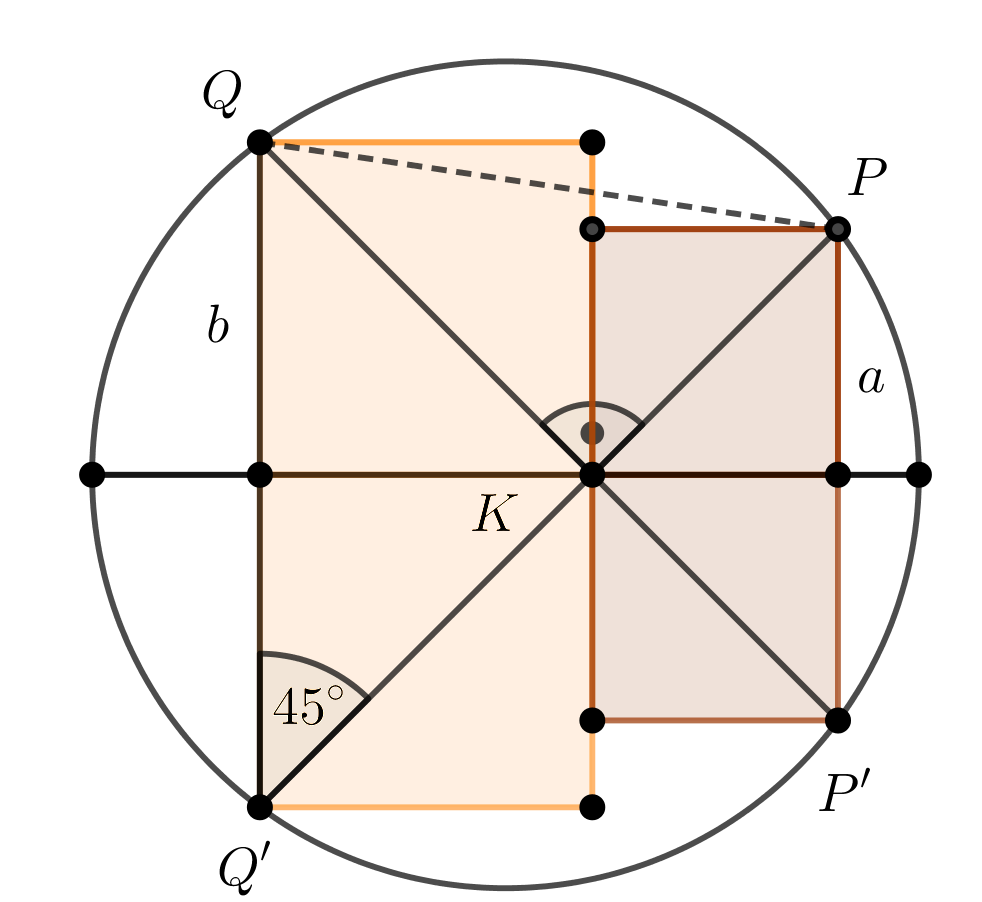
3. ábra
A feltétel szerint \(\displaystyle KP\perp{KQ}\), ezért a tükrözés tulajdonságaiból \(\displaystyle KP'\perp{KQ'}\) következik. Ugyancsak a tükrözés miatt kapjuk azt, hogy \(\displaystyle PQ'\perp{QP'}\), és \(\displaystyle KQ'\) a \(\displaystyle b\) oldalú négyzet tükörképének átlója, ezért
\(\displaystyle KQ'Q\sphericalangle=45^{\circ}.\)
A \(\displaystyle PQ\) húr tehát egy \(\displaystyle 45^{\circ}\)-os kerületi szöghöz tartozó húr, így hossza a sugár \(\displaystyle \sqrt2\)-szöröse, azaz \(\displaystyle PQ=\sqrt{2}\).
Ebből a \(\displaystyle KPQ\) derékszögre felírt Pitagorasz-tétel segítségével kapjuk, hogy
\(\displaystyle \Big(a\sqrt{2}\Big)^2+\Big(b\sqrt{2}\Big)^2=\Big(\sqrt{2}\Big)^2,\)
hiszen \(\displaystyle KP=a\sqrt{2}\) és \(\displaystyle KQ=b\sqrt{2}\).
A műveletek elvégzésével és egyszerűsítéssel adódik, hogy
\(\displaystyle a^2+b^2=1.\)
Eszerint a két négyzet területének összege az egységnyi hosszúságú sugár négyzetével egyenlő, tehát valóban állandó.
Statistics:
116 students sent a solution. 5 points: 57 students. 4 points: 21 students. 3 points: 8 students. 2 points: 6 students. 1 point: 7 students. 0 point: 8 students. Unfair, not evaluated: 3 solutionss. Not shown because of missing birth date or parental permission: 2 solutions.
Problems in Mathematics of KöMaL, March 2023
