 Problem K/C. 767. (April 2023)
Problem K/C. 767. (April 2023)
K/C. 767. The circle \(\displaystyle k\) passes through vertices \(\displaystyle A\), \(\displaystyle B\) of a given square \(\displaystyle ABCD\) in the plane, and touches the side \(\displaystyle CD\). Let \(\displaystyle M\) denote the intersection of circle \(\displaystyle k\) and side \(\displaystyle BC\) which is different from \(\displaystyle B\). Find the exact value of the ratio \(\displaystyle \frac{CM}{BM}\).
Proposed by I. Keszegh, Révkomárom
(5 pont)
Deadline expired on May 10, 2023.
Sorry, the solution is available only in Hungarian. Google translation
1. megoldás. Jelöljük a feladatban szereplő kört \(\displaystyle k\)-val és legyen a \(\displaystyle k\) kör középpontja \(\displaystyle O\). Mivel \(\displaystyle k\) az \(\displaystyle E\) pontban érinti \(\displaystyle CD\)-t, ezért \(\displaystyle OE\) merőleges \(\displaystyle CD\)-re, de akkor \(\displaystyle OE\) egyenese merőleges a \(\displaystyle CD\)-vel párhuzamos \(\displaystyle AB\)-re is. Az \(\displaystyle OE\) tehát a \(\displaystyle k\) kör egy átmérőjének egyenese, és ilyen módon az \(\displaystyle F\) pontban merőlegesen felezi a kör \(\displaystyle AB\) húrját. Ez azt is jelenti, hogy \(\displaystyle OE\) merőlegesen felezi a \(\displaystyle CD\) szakaszt, vagyis \(\displaystyle E\) a \(\displaystyle CD\) felezőpontja. Tekintsük az 1. ábrát, amelyen a négyzet oldalát \(\displaystyle a\)-val, a \(\displaystyle CM\) szakasz hosszát \(\displaystyle x\)-szel jelöltük.
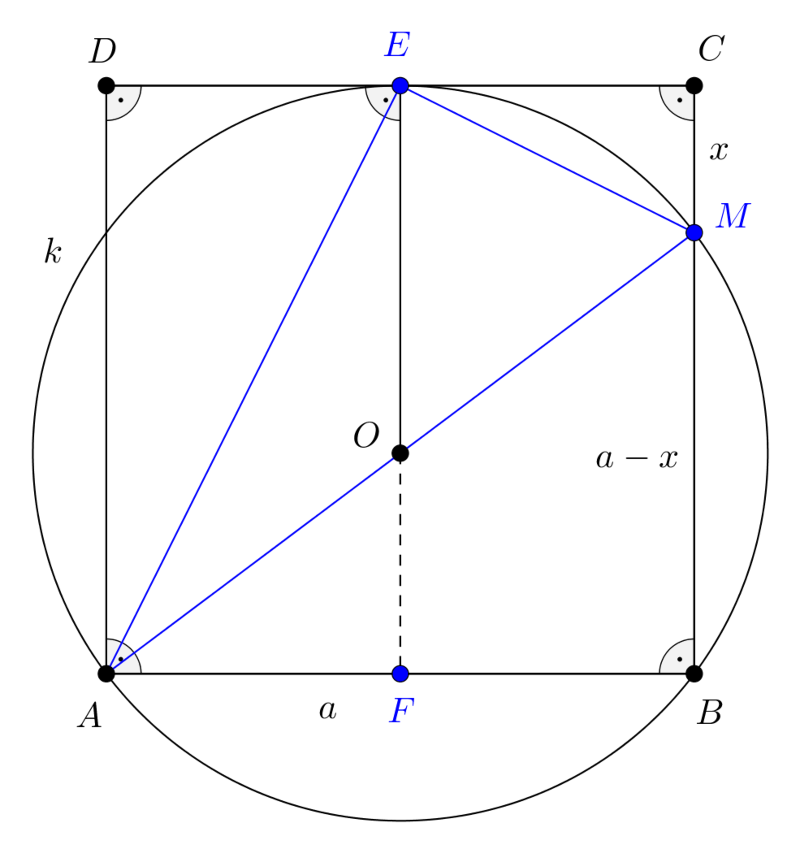
1. ábra
Az \(\displaystyle AM\) szakasz áthalad az \(\displaystyle O\) ponton, hiszen \(\displaystyle ABM\sphericalangle=90^{\circ}\), így a Thalész-tétel megfordítása miatt \(\displaystyle AM\) a kör átmérője. Ebből az is következik, hogy \(\displaystyle AEM\sphericalangle=90^{\circ}\). Az \(\displaystyle AME\) derékszögű háromszögre felírjuk a Pitagorasz-tételt:
| \(\displaystyle (1)\) | \(\displaystyle AE^2+ME^2=AM^2.\) |
Az \(\displaystyle AED\) derékszögű háromszögben \(\displaystyle AD=a\) és \(\displaystyle \displaystyle{ED=\frac{a}{2}}\), ezért a Pitagorasz-tétel alapján
| \(\displaystyle (2)\) | \(\displaystyle \displaystyle{AE^2=a^2+\frac{a^2}{4}}.\) |
Az \(\displaystyle EMC\) derékszögű háromszögből \(\displaystyle \displaystyle{EC=\frac{a}{2}}\) és \(\displaystyle CM=x\) felhasználásával a Pitagorasz-tételből
| \(\displaystyle (3)\) | \(\displaystyle \displaystyle{ME^2=x^2+\frac{a^2}{4}}\) |
következik.
Végül az \(\displaystyle AMB\) derékszögű háromszögből \(\displaystyle AB=a\) és \(\displaystyle BM=a-x\); a Pitagorasz-tétel miatt
| \(\displaystyle (4)\) | \(\displaystyle \displaystyle{AM^2=a^2+\big(a-x\big)^2}.\) |
Behelyettesítjük a (2)-(3)-(4) eredményeket az (1) egyenletbe:
\(\displaystyle \displaystyle{a^2+\frac{a^2}{4}+x^2+\frac{a^2}{4}=a^2+\big(a-x\big)^2},\)
ahonnan a műveletek elvégzésével és rendezéssel
\(\displaystyle \displaystyle{x=\frac{a}{4}}\)
következik. Ez azt jelenti, hogy
\(\displaystyle \displaystyle{\frac{CM}{BM}=\frac{\frac{a}{4}}{\frac{3a}{4}}=\frac{1}{3}},\)
tehát az \(\displaystyle M\) pont a \(\displaystyle BC\) szakasz \(\displaystyle C\)-hez legközelebbi negyedelőpontja.
2. megoldás. Az 1. megoldásban látott módon igazolhatjuk, hogy \(\displaystyle E\) felezőpontja a \(\displaystyle CD\) szakasznak és az \(\displaystyle AM\) szakasz átmérő az \(\displaystyle O\) középpontú \(\displaystyle k\) körben, emiatt \(\displaystyle AEM\sphericalangle=90^{\circ}\).
A következő ábrán a \(\displaystyle CME\sphericalangle=\alpha\) és az \(\displaystyle MEC\sphericalangle=\beta\) jelöléseket alkalmaztuk, amelyekre nyilvánvalóan teljesül, hogy
\(\displaystyle \alpha+\beta=90^{\circ}.\)
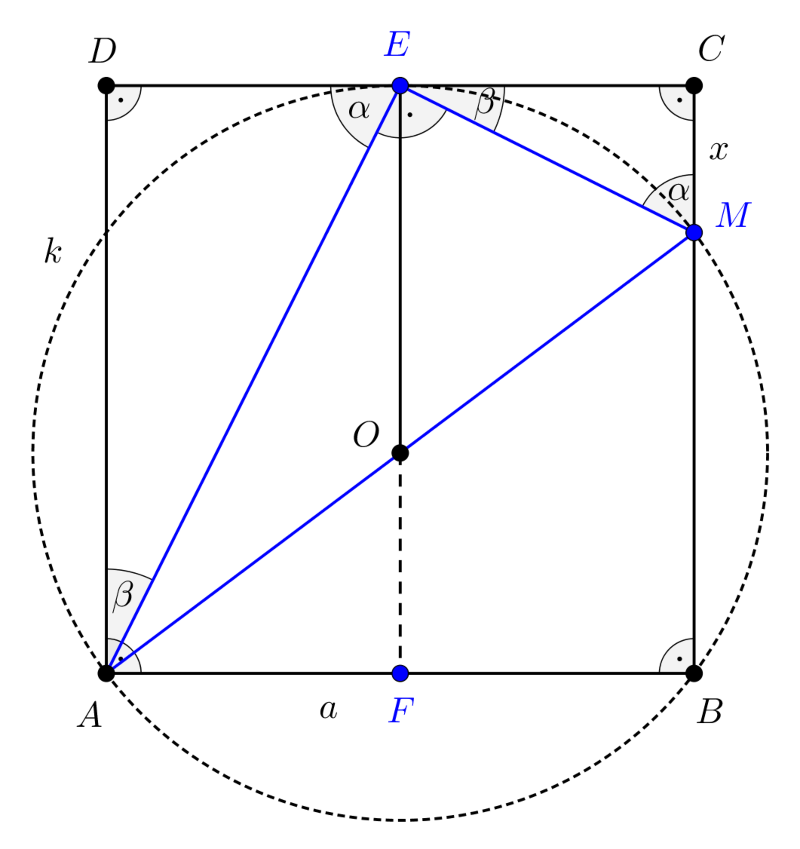
2. ábra
Az \(\displaystyle \alpha+\beta=90^{\circ}\) összefüggés miatt \(\displaystyle AED\sphericalangle=\alpha\) és így \(\displaystyle DAE\sphericalangle=\beta\).
Az \(\displaystyle EMC\) és \(\displaystyle AED\) derékszögű háromszögek megfelelő szögei egyenlők, ez a két háromszög tehát hasonló, ezért a két háromszög megfelelő oldalainak aránya megegyezik. Eszerint: \(\displaystyle \displaystyle{\frac{CM}{CE}=\frac{ED}{AD}}\), azaz \(\displaystyle \displaystyle{\frac{x}{\frac{a}{2}}=\frac{\frac{a}{2}}{a}}\).
Ebből a műveletek elvégzése és egyszerűsítés után adódik, hogy
\(\displaystyle \displaystyle{x=\frac{a}{4}},\)
vagyis az \(\displaystyle M\) pont a \(\displaystyle BC\) szakasz \(\displaystyle C\)-hez legközelebbi negyedelőpontja, tehát
\(\displaystyle \displaystyle{\frac{CM}{BM}=\frac{1}{3}}.\)
Statistics:
92 students sent a solution. 5 points: 54 students. 4 points: 4 students. 3 points: 14 students. 2 points: 2 students. 1 point: 5 students. 0 point: 9 students. Not shown because of missing birth date or parental permission: 1 solutions.
Problems in Mathematics of KöMaL, April 2023
