 Problem K/C. 802. (February 2024)
Problem K/C. 802. (February 2024)
K/C. 802. Let point \(\displaystyle Q\) be an arbitrary inner point of side \(\displaystyle CD\) in square \(\displaystyle ABCD\). Let the perpendicular from vertex \(\displaystyle B\) to line segment \(\displaystyle AQ\) intersect \(\displaystyle AQ\) at \(\displaystyle P\). Let \(\displaystyle K\) denote the intersection point of the diagonals of the square. Prove that line \(\displaystyle PK\) bisects angle \(\displaystyle QPB\).
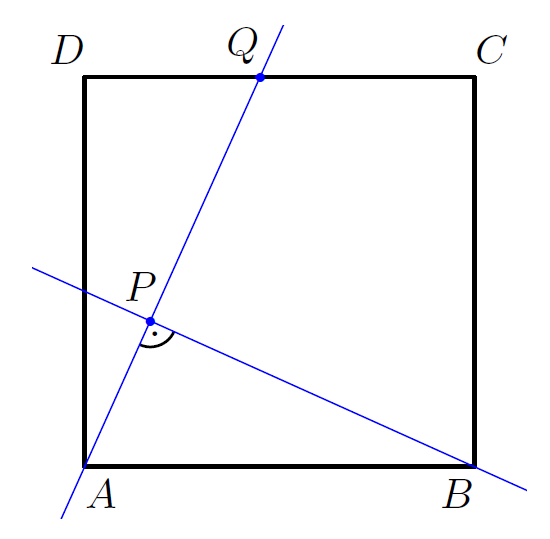
(5 pont)
Deadline expired on March 11, 2024.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. A négyzet átlóinak \(\displaystyle K\) metszéspontja a négyzet szimmetriaközéppontja. Mivel \(\displaystyle Q\) a \(\displaystyle CD\) oldal belső pontja, ezért \(\displaystyle AQ\) biztosan nem megy át a \(\displaystyle K\) ponton, emiatt \(\displaystyle K\) nem illeszkedik a \(\displaystyle BP\) egyenesre sem. Tükrözzük az \(\displaystyle AQ\) és \(\displaystyle BP\) egyeneseket a \(\displaystyle K\) pontra. Tekintsük a következő ábrát, amelyen az \(\displaystyle AQ\) egyenesnek a \(\displaystyle BP\) egyenes tükörképével való metszéspontját \(\displaystyle R\)-rel, a \(\displaystyle BP\) egyenesnek a \(\displaystyle DA\)-val való metszéspontját \(\displaystyle S\)-sel, a megfelelő tükörképpontokat vesszővel jelöltük.
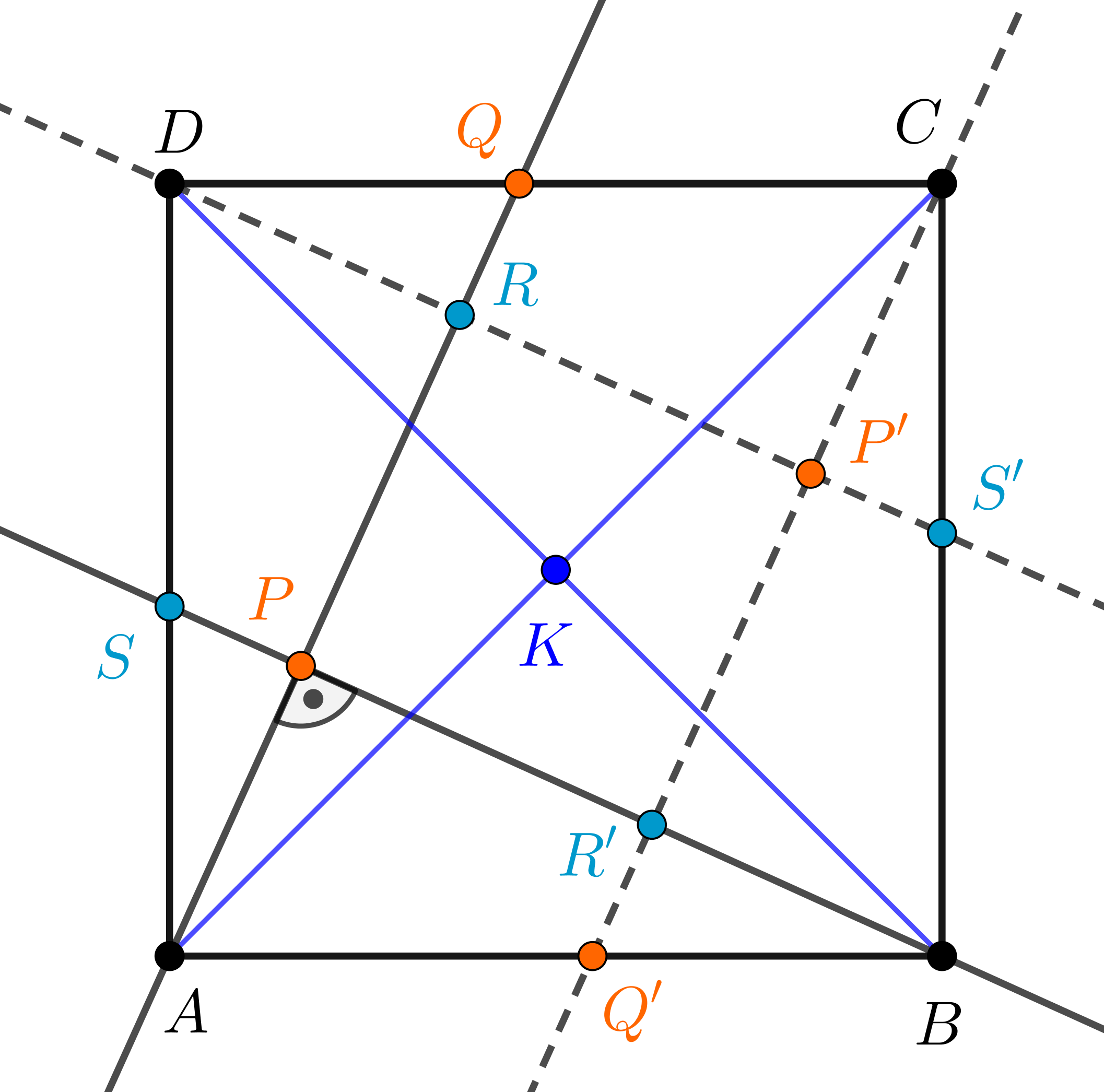
Mivel \(\displaystyle K\) nem illeszkedik az \(\displaystyle AQ\) egyenesre, ezért \(\displaystyle AQ\parallel CQ'\), hiszen \(\displaystyle A\) tükörképe \(\displaystyle C\). Hasonlóképpen a \(\displaystyle BS\) egyenesre sem illeszkedik \(\displaystyle K\), így \(\displaystyle BS\parallel DS'\), mivel \(\displaystyle B\)-nek \(\displaystyle K\)-ra vonatkozó tükörképe \(\displaystyle D\). Ez az \(\displaystyle APB\sphericalangle=90^{\circ}\) miatt azt jelenti, hogy a \(\displaystyle PR'P'R\) négyszög szögei derékszögek, tehát téglalap. Bizonyítani fogjuk, hogy \(\displaystyle PR'P'R\) négyzet.
A \(\displaystyle BSA\) és \(\displaystyle AQD\) derékszögű háromszögek egybevágók, mert \(\displaystyle ABS\sphericalangle\) és \(\displaystyle QAD\sphericalangle\) merőleges szárú hegyesszögek és így \(\displaystyle ASB\sphericalangle=AQD\sphericalangle\) is igaz, másrészt a megfelelő szögekkel szemközti \(\displaystyle AB\) és \(\displaystyle DA\) oldalak hossza egyenlő.
Ez azt is jelenti, hogy \(\displaystyle AS=DQ\) és ezért \(\displaystyle DS=CQ\). Az \(\displaystyle AQCQ'\) és \(\displaystyle DSBS'\) négyszögek a tükrözés miatt paralelogrammák, szögeik \(\displaystyle ASB\sphericalangle=AQD\sphericalangle\) miatt egyenlők, így \(\displaystyle DS=CQ\), illetve \(\displaystyle BS=AQ\) miatt a paralelogrammák egybevágók is. Eszerint az \(\displaystyle AQCQ'\) paralelogrammának az \(\displaystyle AQ\) oldalhoz tartozó magassága ugyanolyan hosszú, mint a \(\displaystyle DSBS'\) paralelogramma \(\displaystyle BS\) oldalához tartozó magassága, vagyis
\(\displaystyle PR'=PR,\)
ez éppen azt jelenti, hogy a \(\displaystyle PR'P'R\) téglalap négyzet, amelynek szimmetriaközéppontja \(\displaystyle K\). Ebből azonnal következik, hogy \(\displaystyle PK\) felezi a \(\displaystyle QPB\) derékszöget.
Statistics:
Problems in Mathematics of KöMaL, February 2024
